Authors:
Paper:
https://arxiv.org/abs/2408.10543
Introduction
Background
Point clouds, consisting of numerous discrete points with coordinates (x, y, z) and optional attributes, offer a flexible representation of diverse 3D shapes. They are extensively applied in various fields such as autonomous driving, game rendering, and robotics. With the rapid advancement of point cloud acquisition technologies and 3D applications, effective point cloud compression techniques have become indispensable to reduce transmission and storage costs.
Problem Statement
Traditional point cloud compression methods, such as G-PCC and V-PCC, have limitations in capturing the intricate diversity of point cloud shapes, often yielding blurry and detail-deficient reconstructions. Recent advancements in deep learning, particularly Variational Autoencoders (VAEs), have shown promise but still face challenges in producing high-quality reconstructions due to feature homogenization and inadequate latent space representations.
Related Work
Point Cloud Compression
Classic point cloud compression standards like G-PCC employ octree structures to compress geometric information. Recent methods inspired by deep learning have focused on voxel-based and point-based approaches. Voxel-based methods include sparse convolution and octree-based techniques, while point-based methods utilize symmetric operators to handle permutation-invariant point clouds and capture geometric shapes. These methods are categorized into lossy and lossless types based on different quantization operations.
Diffusion Models for Point Cloud
Diffusion models have recently gained attention for their outstanding performance in generating high-quality samples and adapting to intricate data distributions. These models have been explored in point cloud applications, such as DPM, PVD, LION, Dit-3D, PDR, Point·E, PointInfinity, and DiffComplete. These advancements demonstrate the promise of diffusion models in point cloud generation tasks, motivating the exploration of their applicability in point cloud compression.
Research Methodology
Overview
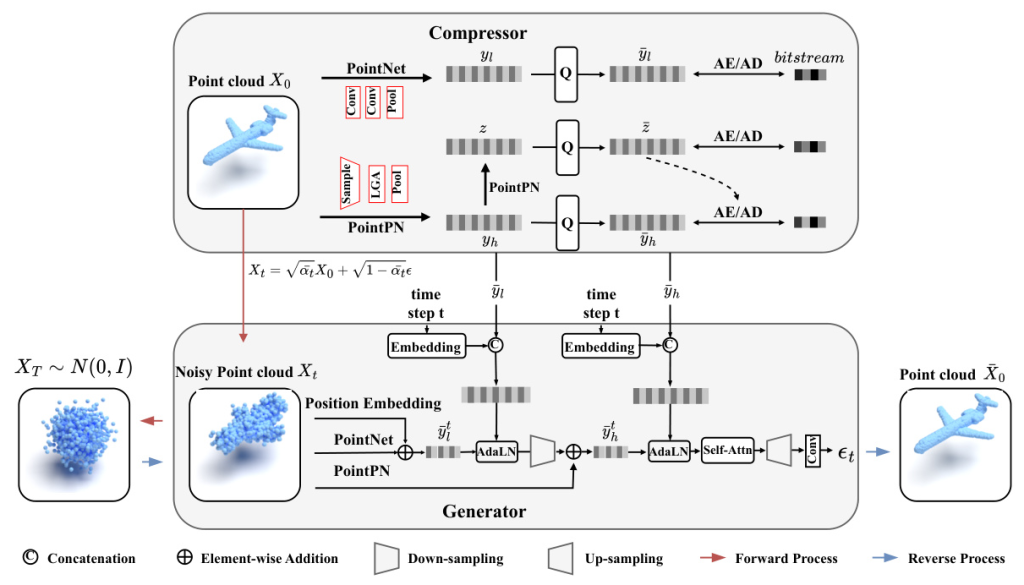
The proposed Diff-PCC framework leverages diffusion models to achieve superior rate-distortion performance with exceptional reconstruction quality. It introduces a dual-space latent representation that employs two independent encoding backbones to extract complementary shape latents from distinct latent spaces. At the decoding side, a diffusion-based generator produces high-quality reconstructions by considering the shape latents as guidance to stochastically denoise the noisy point clouds.
Preliminaries
Denoising Diffusion Probabilistic Models (DDPMs) comprise two Markov chains: the diffusion process and the denoising process. The diffusion process adds noise to clean data, resulting in a series of noisy samples. The denoising process is the reverse process, gradually removing the noise added during the diffusion process.
Dual-Space Latent Encoding
The compressor in Diff-PCC extracts expressive shape latents from distinct latent spaces using two independent encoding backbones. PointNet is used to extract low-frequency shape latents, while PointPN characterizes complementary latents from the high-frequency domain. The quantized features are then compressed into bitstreams using fully factorized and hyperprior density models.
Diffusion-based Generator
The generator takes noisy point clouds and necessary conditional information as input. It learns the positional distribution of the noisy point clouds and integrates it with the conditional information to predict noise at each time step. The generator uses a hierarchical feature fusion mechanism and self-attention to interact with information from different local areas, generating high-quality reconstructions.
Experimental Design
Experimental Setup
The experiments were conducted using the ShapeNet dataset for training and ModelNet10 and ModelNet40 datasets for testing. The model was implemented using PyTorch and CompressAI, trained on an NVIDIA 4090X GPU for 80,000 steps with a batch size of 48. The Adam optimizer was used with an initial learning rate of 1e-4 and a decay factor of 0.5 every 30,000 steps.
Baselines & Metrics
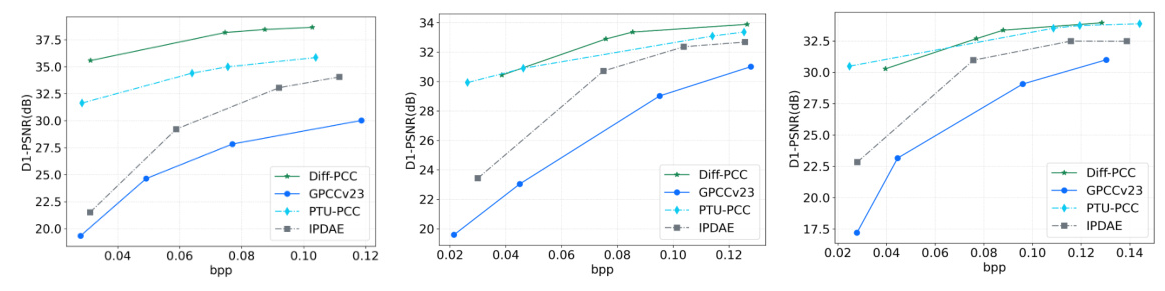
The proposed method was compared with state-of-the-art non-learning-based methods (G-PCC) and the latest learning-based methods (IPDAE, PCT-PCC). Point-to-point PSNR was used to measure geometric accuracy, and the number of bits per point was used to measure the compression ratio.
Results and Analysis
Objective Quality Comparison
The quantitative indicators using BD-Rate and BD-PSNR, and the rate-distortion curves of different methods, demonstrate that Diff-PCC achieves superior rate-distortion performance. It conserves between 56% to 99% of the bitstream compared to G-PCC and surpasses G-PCC by 7.711 dB in point-to-point PSNR at the most minimal bit rates.
Subjective Quality Comparison
The ground truth and decoded point clouds from different methods reveal that Diff-PCC preserves the shape information of the ground truth to the greatest extent while achieving the highest PSNR.

Ablation Studies
Ablation studies examined the impact of key components in the model. The results indicate that high-frequency features play an effective role in guiding the model during the reconstruction process, while low-frequency features are crucial for preserving the shape of the point cloud. The loss function designed in the study also contributes to the overall performance.

Overall Conclusion
The proposed Diff-PCC method leverages the expressive power of diffusion models for generative and aesthetically superior decoding of 3D point clouds. By introducing a dual-space latent representation and an effective diffusion-based generator, Diff-PCC achieves state-of-the-art compression performance and superior subjective quality. Future work may focus on reducing coding complexity and extending the method to handle large-scale point cloud instances.