Authors:
Huajian Xin、Z.Z. Ren、Junxiao Song、Zhihong Shao、Wanjia Zhao、Haocheng Wang、Bo Liu、Liyue Zhang、Xuan Lu、Qiushi Du、Wenjun Gao、Qihao Zhu、Dejian Yang、Zhibin Gou、Z.F. Wu、Fuli Luo、Chong Ruan
Paper:
https://arxiv.org/abs/2408.08152
Introduction
Recent advancements in large language models have significantly influenced mathematical reasoning and theorem proving in artificial intelligence. Despite notable progress in natural language domains, language models still encounter substantial challenges in formal theorem proving, such as using Lean and Isabelle, which require rigorous derivations satisfying formal specifications of the verification system. Even advanced models like GPT-4 struggle with complex formal proofs, underscoring the intricate nature of both the coding and the mathematics involved.
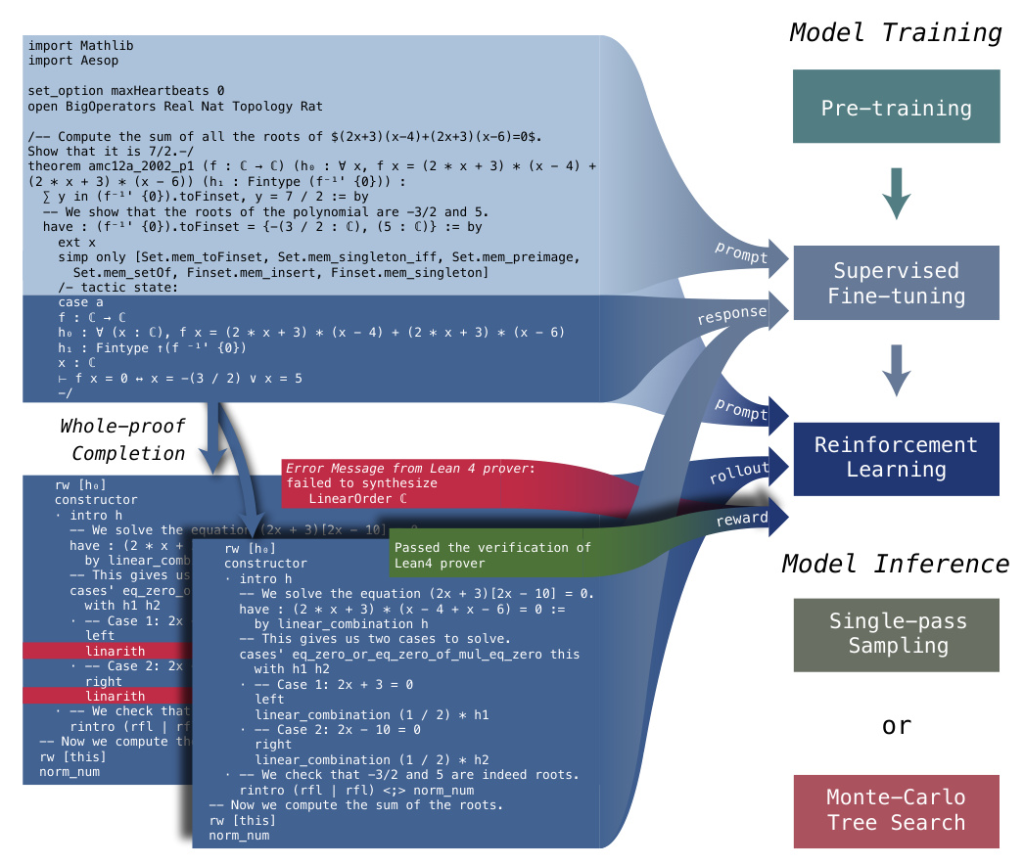
Language models in formal theorem proving typically employ two strategies: proof-step generation and whole-proof generation. Proof-step generation predicts each subsequent tactic and verifies it using the formal verifier to obtain updated information about the current tactic state, often utilizing tree search techniques to construct valid proofs. In contrast, whole-proof generation is computationally efficient, producing an entire proof code based on the theorem statement, requiring less communication budget to coordinate between the prover model and the formal theorem verifier.
To seamlessly integrate intermediate tactic states in proof-step generation while maintaining the simplicity and computational efficiency of whole-proof generation, we have developed a unified approach in DeepSeek-Prover-V1.5. This method combines the strengths of both proof-step and whole-proof generation techniques through a truncate-and-resume mechanism. The process begins with standard whole-proof generation, where the language model completes the proof code following the theorem statement prefix. The Lean prover then verifies this code. If the proof is correct and complete, the procedure terminates. If an error is detected, the code is truncated at the first error message, and any subsequent code is discarded. The successfully generated proof code is then used as a prompt for the generation of the next proof segment. To enhance the accuracy of the model’s new completions, we append the latest state from the Lean 4 prover as a comment at the end of the prompt.
Model Training
Pre-training
To enhance our language model’s proficiency in generating formal proofs and reasoning through mathematical language, we further pre-train our base model. This refinement involved training on high-quality datasets that include both code and natural language mathematical content. We specifically focused on formal languages widely used in proof assistants, such as Lean, Isabelle, and Metamath. We designate this improved model as DeepSeek-Prover-V1.5-Base.
Supervised Fine-tuning
In this section, we explore the methodology and processes involved in the supervised fine-tuning (SFT) of DeepSeek-Prover-V1.5. Specifically, we augment the proof dataset from DeepSeek-Prover-V1 by adding detailed explanatory comments. This enhancement aims to improve the alignment between natural language descriptions and Lean 4 code, thereby facilitating better formal mathematical reasoning. Additionally, we incorporate intermediate tactic state information as an auxiliary prediction task to support the truncate-and-resume mechanism used in the Monte-Carlo Tree Search process. We refer to the resulting model as DeepSeek-Prover-V1.5-SFT.
Data Curation: We develop a comprehensive Lean 4 code completion dataset for the supervised fine-tuning. This dataset includes synthetic proof code derived from a wide range of formal theorems. These theorems are sourced from various projects, such as the standard Lean 4 math library Mathlib4, synthetic theorems from DeepSeek-Prover-V1, and validation sets from the miniF2F and ProofNet benchmarks. To augment the formal proof data, we employed an expert iteration process. This involves generating proofs using the language model, verifying the generated proof data, retraining the model with the verified data, and then using the optimized model to generate additional proof data. The resulting proof dataset consists of 9,645k sequences.
Thought-augmented Proof Generation: In DeepSeek-Prover-V1, we identified a significant gap between problem-solving strategies in natural language and theorem proving in Lean. In natural language, models generate detailed deduction steps to construct proofs, whereas in Lean, they often rely on a sequence of high-level tactic calls to brute-force solutions. These high-level tactics, while effective, obscure their internal workings and outcomes, hindering the model’s ability to resolve complex proof goals with structured mathematical reasoning. To address this issue, we develop an approach that incorporates natural language reasoning before generating theorem proof code. Similar to Lean-STaR, which performs isolated chain-of-thought reasoning before each proof step, our method integrates this reasoning directly as comments within the proof code.
Prompt Augmentation with Tactic State Information: To implement the truncate-and-resume mechanism for Monte-Carlo Tree Search, we needed to extract tactic information from the code generated by the model. We enhanced the Lean REPL with data extraction tools from the LeanDojo project. This allowed us to extract tactic information in triples, which include the position of each tactic, as well as the tactic states before and after its application. This information helps us identify the specific tactic code that triggers verification errors. For each tactic in a generated valid formal proof, we insert the tactic state returned by the verifier as a comment “/- tactic state: … -/”. During training, we use all tokens following “/- tactic state: ” as responses to calculate the supervised fine-tuning loss, while the tokens before this comment are used as prompts and do not contribute to the training loss calculation.
Training Setting: We conduct supervised fine-tuning based on the pre-trained model and train for 9B tokens, using a batch size of 2,048 and a constant learning rate of 1e-4. The training process begins with 100 warm-up steps to stabilize the learning dynamics. Training examples are randomly concatenated to form sequences, with a maximum context length of 4,096 tokens.
Reinforcement Learning from Proof Assistant Feedback
Reinforcement learning (RL) has been proven effective in enhancing the mathematical reasoning capabilities of supervised fine-tuned language models. To further advance DeepSeek-Prover-V1.5-SFT, we incorporate a reinforcement learning phase, resulting in the model DeepSeek-Prover-V1.5-RL. This phase leverages RL to enhance performance based on verification feedback from the Lean 4 prover.
Prompts: In the reinforcement learning stage, we use a subset of theorem statements from the supervised fine-tuning dataset as training prompts. We select theorems for which DeepSeek-Prover-V1.5-SFT has a moderate success rate in generating correct proofs upon multiple attempts. This ensures that the model has room for improvement while still being able to receive positive feedback. After filtering, we retain approximately 4.5k unique theorem statements. Each theorem is prefixed with both CoT and non-CoT guiding prompts to enhance the model’s proof generation capabilities in both modes.
Rewards: When training LLMs via RL, a trained reward model typically provides feedback signals. In contrast, formal theorem proving benefits from the rigorous verification of generated proofs by proof assistants, offering a significant advantage. Specifically, each generated proof receives a reward of 1 if verified as correct, and 0 otherwise. While this binary reward signal is accurate, it is also sparse, especially for theorems that are challenging for the supervised fine-tuned model. To mitigate this sparsity, we select training prompts that are challenging yet achievable for the supervised fine-tuned model.
Reinforcement Learning Algorithm: We employ the Group Relative Policy Optimization (GRPO) as our RL algorithm, which has demonstrated superior effectiveness and efficiency compared to PPO, primarily because it eliminates the necessity of training an additional critic model. Specifically, GRPO samples a group of candidate proofs for each theorem prompt and optimizes the model based on the relative rewards of the outputs within the group. Our prompt selection strategy is designed to likely include both correct and incorrect proofs among the candidates, aligning well with the group-relative nature of GRPO and thereby enhancing the training process.
Training Setting: We conduct RL training based on the SFT model, which serves as both the initial model and the reference model for imposing the Kullback-Leibler (KL) divergence penalty. We use a constant learning rate of 5e-6, and the KL penalty coefficient is set to 0.02. For each theorem, we sample a group of 32 candidate proofs, with maximum length set to 2,048. The training batch size is configured to 512.
Evaluation
Benchmarks
We evaluate theorem-proving performance on the following benchmarks to compare model capabilities after each training stage:
- MiniF2F: Focuses on formal problem-solving skills for high-school level exercises and competitions, such as AMC, AIME, and IMO, with an emphasis on algebra and number theory. The benchmark includes 244 validation and 244 test problems, originally in Lean 3 and manually converted to Lean 4.9.0.
- ProofNet: Evaluates formal theorem-proving capabilities at the undergraduate level in mathematics. It comprises 185 validation and 186 test problems from widely-used undergraduate textbooks, covering real and complex analysis, linear algebra, abstract algebra, and topology. These problems were initially in Lean 3 and manually converted to Lean 4.9.0.
Prompting Configurations
For each proof attempt of DeepSeek-Prover-V1.5-Base, we independently sample three proof demonstrations from the validation set to construct the few-shot prompts. For the miniF2F benchmark, we use human-written proofs, while for the ProofNet benchmark, we use correct proofs generated by DeepSeek-Prover-V1.5-RL as few-shot demonstrations. For DeepSeek-Prover-V1.5-SFT and DeepSeek-Prover-V1.5-RL, we employ two types of guiding prompts: one that encourages chain-of-thought (CoT) reasoning before each proof step, and one that does not (non-CoT).
Metric
We evaluate theorem-proving performance using the pass@𝐾 accuracy metric, which measures the model’s success in generating a correct proof within 𝐾 attempts. Each model is deployed on a single A100-40G GPU, utilizing the vLLM framework for sample generation. The sampling parameters are set with a temperature of 1, a top-p value of 0.95, and a maximum token limit of 2,048. The generated proofs are then verified using the Lean 4 theorem prover. For this verification, we import Mathlib4 and Aesop to access predefined premises and tactics. The verification process is subject to a time limit of 300 seconds.
Comparison across Training Stages
Figure 3 presents a comparative analysis of each training stage on the miniF2F and ProofNet datasets. Our base model, DeepSeek-Prover-V1.5-Base, achieves a notable pass rate, solving nearly one-third of the problems on the test set of the miniF2F benchmark using 3-shot prompting. The supervised fine-tuning stage, resulting in DeepSeek-Prover-V1.5-SFT, significantly outperforms the base model, with Pass@128 accuracy increasing by approximately two-thirds on miniF2F and doubling on ProofNet. The subsequent reinforcement learning stage further enhances the model’s performance, improving Pass@𝐾 accuracy across all values of 𝐾.
Comparison between CoT and non-CoT
We compare the performance of non-CoT and CoT generation modes for both DeepSeek-Prover-V1.5-SFT and DeepSeek-Prover-V1.5-RL. The results in Figure 3 demonstrate that the CoT mode consistently outperforms the non-CoT mode across most settings. Specifically, DeepSeek-Prover-V1.5-RL, leveraging these enhanced theorem-proving patterns, achieves superior performance on both benchmarks, with an average accuracy of 51.6% on miniF2F and 18.2% on ProofNet. The integration of natural language reasoning in CoT mode significantly enhances the planning and execution of formal proof writing.
Exploration-oriented Monte-Carlo Tree Search
Tactic-level Tree Abstraction
To implement the tree search method in the whole-proof generation setting, we introduce a proof tree abstraction to define the tailored state and action space, leveraging a truncate-and-resume mechanism. Roughly following the paradigm of Yao et al., we begin by decomposing an incomplete proof into a sequence of tree nodes that correspond to individual proof steps, and then we utilize the partial content stored in these tree nodes to continue the proof generation process.
Truncate: Proof Decomposition into Tree Nodes: We construct the proof search tree at the tactic level, where each tree edge represents a single transition step of the tactic state. Initially, we submit the entire proof the model generated to the Lean prover to parse it into tactics. We then truncate the proof at the earliest verification error, ensuring that all subsequent tactic codes can be successfully applied to advance the proof towards the desired theorem. The tactic codes are segmented into several code fractions, each containing a valid tactic code and its associated chain-of-thought comments, corresponding to a single tree edge that represents a tactic state transition. Through this abstraction, each tactic code is converted into a series of tree nodes, forming a path from the root to a specific node.
Resume: Proof Generation from a Tree Node: In Lean 4, different tactics can lead to the same tactic state, meaning each node in our proof tree can correspond to various tactic codes that achieve the same outcome. To handle this, we store a set of these equivalent tactic codes at each node. When the tree search agent expands a node, it randomly selects one tactic to use as a prompt for the language model. This prompt includes the incomplete proof code ending with the chosen tactic and the tactic state information from the Lean prover as a comment block. The fine-tuned model has been trained to recognize and utilize this format, using the incomplete code augmented with tactic state comments to guide subsequent proof generation.
Interactive Theorem Proving via Monte-Carlo Tree Search
Our proof search tree is developed using the standard Monte-Carlo Tree Search (MCTS) paradigm, which iteratively applies four steps: Selection, Expansion, Simulation, and Backpropagation. We integrate the Simulation step into Expansion because our whole-proof generation model inherently performs a rollout from the expanded node. The detailed design of the algorithm workflow is as follows.
Selection: The selection step, also known as the tree policy, starts from the root node and traverses downward to identify a promising node for expansion. The objective of this algorithmic step is to trade off between exploration and exploitation. The tree policy at a tree node is computed by selecting the action that maximizes the value from the set of valid operations.
Expansion: The next step is invoking the proof generation model to expand the node nominated by the selection phase. Resuming the incomplete proof codes stored on the node designated for expansion, we perform whole-proof generation to propose a series of subsequent tactics and submit the generated proof to Lean prover for verification. Such a trial of proof completion is equivalent to conducting a single rollout of simulation within the standard MCTS framework. When the verification result indicates the proof is complete, the search procedure is ready to be terminated, having found a new proof of the desired theorem. Otherwise, we parse the verification feedback and truncate the generated proof to the assertion of the earliest verification error. The remaining tactics are transformed into a path of nodes to be merged into the search tree.
Backpropagation: The final phase of each tree search iteration is to update value statistics along the selection trajectory from the root to the expanded node, i.e., updating the values associated with the tree policy. The extrinsic source of rewards comes from the compiler feedback, specifically assigning a reward of 1 for completed proofs and 0 for unsolved ones. In Section 3.3, we will introduce an intrinsic reward mechanism to augment the reward assignment that enhances the agent’s incentive for exploration.
Intrinsic Rewards for Monte-Carlo Tree Search
In the search problem of formal theorem proving, the extrinsic rewards are extremely sparse, i.e., the search agent only obtains non-zero rewards when the proof is completely solved. More specifically, the proof search process forms a tree structure with only a narrow set of leaves delivering non-zero rewards, which matches a famous hard-exploration case in the literature of statistical reinforcement learning. To promote exploration in sparse-reward sequential decision making, one classical paradigm is constructing intrinsic rewards that encourage the agent to not only optimize extrinsic rewards but also acquire general information about the interactive environment.
RMax applied to MCTS: We adopt RMax, a classical exploration mechanism, to construct intrinsic rewards for Monte-Carlo tree search. The core idea of RMax is to explore a broad coverage of the state space. The agent awards itself a maximal amount of reward upon reaching an unseen state. In the context of proof search, where no extrinsic rewards are provided until the proof is completed, our algorithmic procedure resembles ZeroRMax, in which the agent’s exploration is driven solely by intrinsic rewards. The intrinsic reward of a tree expansion step is determined by whether a new node is added to the search tree.
UCB for Non-stationary Rewards: The common setting of UCB exploration bonus for Monte-Carlo tree search is using UCB1. To facilitate discussions, we propose to use an alternative variant of UCB method. Note that the derived intrinsic reward is a non-stationary reward signal whose expected value decays with the progress of exploration. That is because it becomes definitely harder to discover new nodes with unseen tactic states as the search tree expands through sophisticated exploration. To tackle the non-stationarity, we consider discounted upper confidence bounds (DUCB), which uses a discount factor to smoothly drop those outdated feedback records.
Parallelization of Monte-Carlo Tree Search
To enhance the efficiency of Monte-Carlo Tree Search (MCTS), we implement several established parallelization techniques.
- Root Parallelization: We deploy 256 MCTS runners per node, with one language model per GPU and a batch size of 512 for proof generation. The Lean prover is invoked through REPL and executed on a cluster with thousands of CPU cores, where each proof verification task is handled by an individual process, created and terminated in a sandbox. Both proof generation by language models and verification by Lean provers are handled asynchronously. This setup allows MCTS runners to perform concurrent tree search operations, significantly accelerating the process.
- Tree Parallelization: We manage each search tree with 32 thread workers to parallelize the tree iteration steps. This method effectively schedules and balances the tasks of proof generation and Lean verification. Each thread worker iteratively performs the tree search loop by selecting a candidate node for expansion, invoking the language model to generate the proof, verifying the generated proof with the Lean prover, and performing backpropagation.
- Virtual Loss: To encourage diverse node selection among concurrent thread workers, we assign a virtual reward of 0 for ongoing iterations. This involves backpropagating a reward of 0 temporarily and updating it to the true reward upon completion. This strategy promotes exploration of different nodes for expansion, thereby enhancing the overall search efficiency.
Comparison with Existing Methods
In this section, we compare our proposed proof tree search method, which introduces a novel truncate-and-resume mechanism for whole-proof generation, with existing approaches. Current methods for using language models in formal mathematics proof search generally fall into two main strategies:
- Multi-pass proof-step generation: This strategy breaks down the proving process into multiple episodes of tactic generation and verification, typically following a tree search pattern. It involves generating and verifying one tactic at a time, repeating the process for the next tactic until no proof goals remain.
- Single-pass whole-proof generation: This approach generates and verifies an entire proof in one attempt. If the proof is incorrect, the model generates a new proof in the next attempt.
Our proof tree search method uniquely bridges these two strategies, offering a novel hybrid approach. It starts with whole-proof generation, similar to the single-pass approach, but extends this by implementing a sophisticated truncate-and-resume