Authors:

Ilya Kuleshov、Galina Boeva、Vladislav Zhuzhel、Evgenia Romanenkova、Evgeni Vorsin、Alexey Zaytsev

Paper:

https://arxiv.org/abs/2408.08055

COTODE: COntinuous Trajectory Neural Ordinary Differential Equations for Modelling Event Sequences

Introduction

Event sequences are prevalent in various domains, such as banking transactions, medical histories, sales data, and earthquake records. These sequences often exhibit uneven structures, posing challenges for traditional processing algorithms. While conventional methods model hidden data dynamics as probabilistic processes, recent advancements have explored the use of Neural Ordinary Differential Equations (ODEs) to process sequential data. This paper introduces COTODE, a novel approach that models event sequences through continuous trajectories using Neural ODEs, addressing the limitations of discontinuous trajectories in previous methods.

Related Works

Neural Network Approaches

Deep learning methods, particularly Recurrent Neural Networks (RNNs) and transformers, have been applied to event sequences. However, these methods often overlook the irregularity inherent in event sequences. More advanced works integrate Temporal Point Processes (TPP) theory with neural networks, but they are limited in the types of processes they can represent.

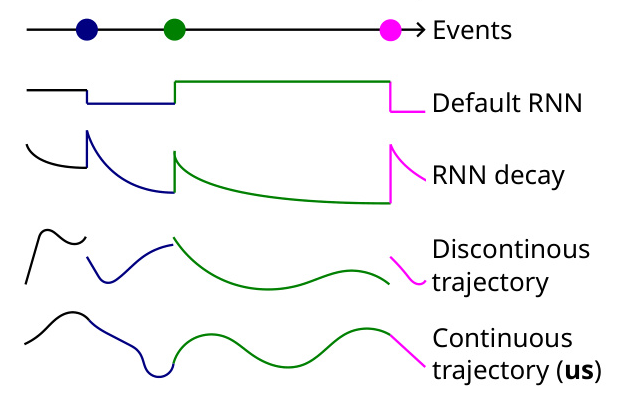
Discontinuous-Trajectory Neural ODEs

Previous works have applied Neural ODEs to event sequences, but they typically result in discontinuous hidden trajectories. These methods introduce jumps at event times, which can be detrimental to model quality. The proposed COTODE model aims to fill this gap by generating continuous hidden trajectories, avoiding the need for disruptive jumps.

Continuous-Trajectory Neural ODEs

Continuous trajectory models, such as those based on Controlled Differential Equations (CDEs), have been proposed for continuous processes. However, these models impose certain restrictions and are not directly applicable to event sequences. COTODE extends this idea to event sequences, ensuring continuous evolution of the hidden state.

Gaussian Process Regression Errors

Gaussian Process (GP) interpolation is used to estimate the uncertainty in the hidden state due to unobserved events. This theoretical analysis provides error bounds for the proposed model, highlighting the limitations of raw ODE-based methods and motivating the introduction of negative feedback.

Methods

COTODE Pipeline

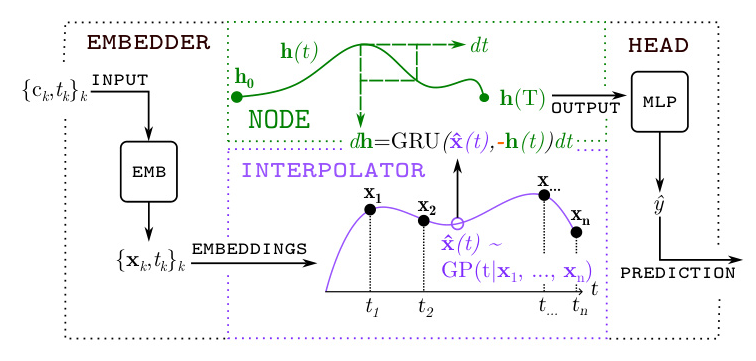
The COTODE pipeline consists of three main components: the Embedder, the Backbone, and the Head. The Embedder converts categorical features into vectors, the Backbone processes these vectors using a Neural ODE-based architecture, and the Head transforms the final hidden state into predictions. The key contribution is the use of GP interpolation to generate a continuous trajectory for the input data.

Neural ODE Overview

The Neural ODE layer propagates the hidden state by solving a Cauchy problem, with the dynamics function defined by a neural network. The input data is fed to the dynamics as an interpolation function, resulting in a continuous hidden trajectory.

Interpolation of the Hidden Trajectory

GP interpolation is used to define the influence of events in the gaps between them. This method provides error bounds for the final hidden state, quantifying the uncertainty due to unobserved events.

GRU Negative Feedback

To address the issue of linearly growing error, a negative feedback mechanism inspired by the Gated Recurrent Unit (GRU) architecture is introduced. This modification ensures numerical stability and limits the growth of error in the hidden trajectory.

Experiments

Data

The experiments are conducted on six datasets, including four transactional datasets (Age, Churn, HSBC, Gender) and two non-transactional datasets (WISDM Human Activity Classification, Retail). These datasets vary in their target labels and sequence lengths, providing a comprehensive evaluation of the proposed model.

Models

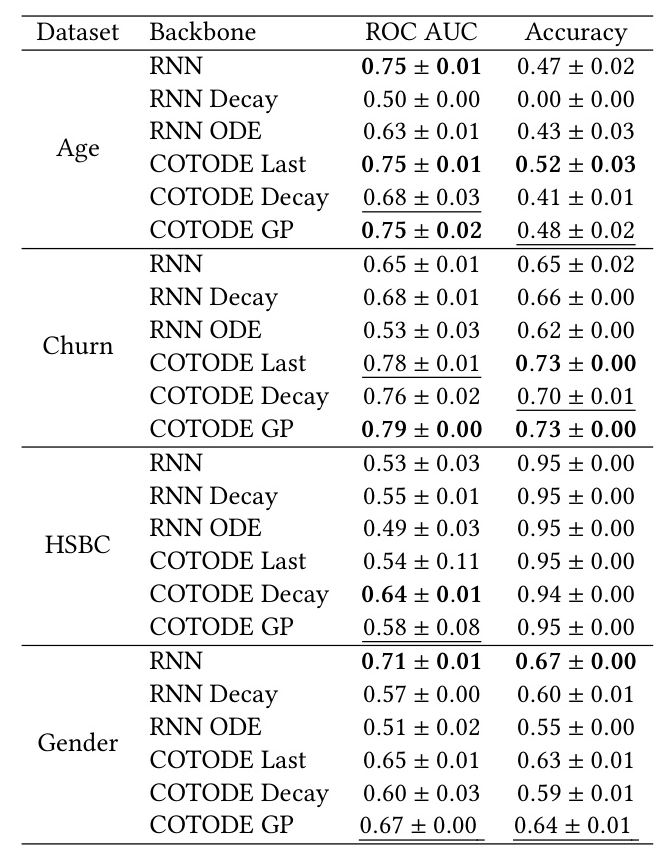
The performance of six models is compared, including the vanilla GRU, RNN Decay, RNN ODE, and three variations of the COTODE model (GP, Last, Decay). The categorical features are encoded into learnable embeddings, and the time since the last transaction is appended to the input vector.

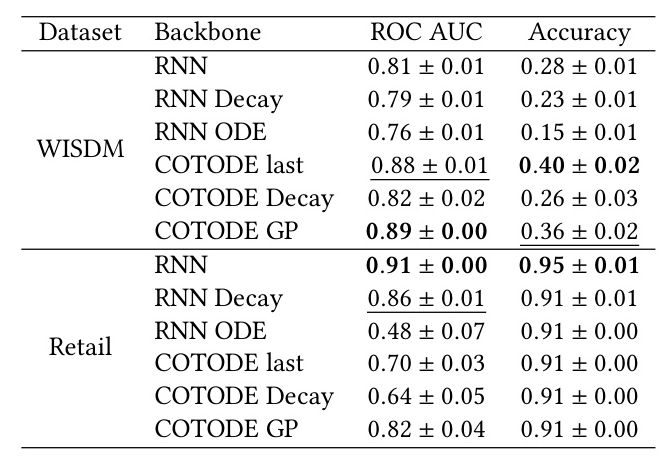
Results

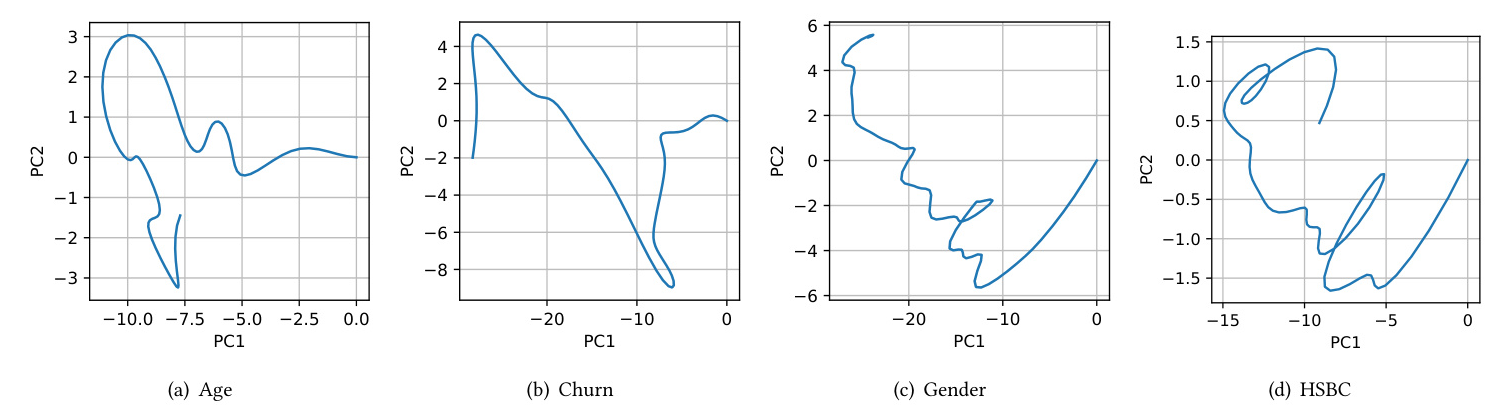
The results demonstrate the superior performance of the COTODE model with GP interpolation on most datasets. The proposed method achieves up to 20% improvement in ROC-AUC compared to other models. The generated continuous trajectories reflect the complexities of diverse datasets, indicating the model’s ability to capture the underlying dynamics.

Ablation Study

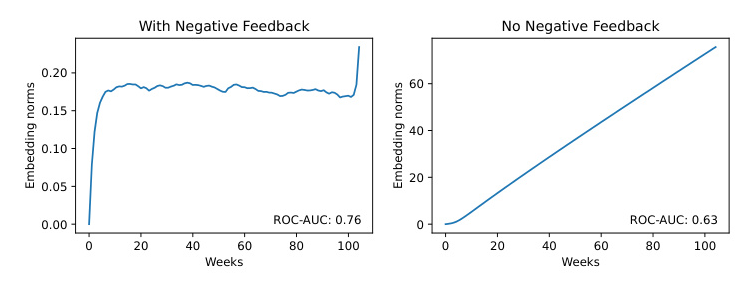
Negative Feedback

The effect of the GRU-based negative feedback is evaluated by comparing the embedding norms across the trajectory with and without the modification. The results show that the proposed negative feedback significantly improves model stability and performance.

Other Interpolation Regimes

Two alternative interpolation regimes (Last and Decay) are compared with the GP-based approach. While these variations perform on par with the GP method on some datasets, they show significant drops in quality on others, highlighting the importance of GP interpolation for the success of the model.

Conclusions

COTODE presents a novel approach to modelling event sequences through continuous trajectories using Neural ODEs. By integrating GP interpolation and negative feedback, the proposed method addresses the limitations of previous models and achieves state-of-the-art performance on various datasets. The theoretical analysis provides error bounds for the model, ensuring robustness and stability in practice.