Authors:
Paper:
https://arxiv.org/abs/2408.10369
Boolean Matrix Logic Programming: A Detailed Exploration
Introduction
Boolean Matrix Logic Programming (BMLP) is an innovative approach to datalog query evaluation that leverages the power of boolean matrix operations. Traditional datalog query evaluations have primarily focused on symbolic computations. However, recent studies have demonstrated that matrix operations can significantly enhance the performance of datalog query evaluations. This paper introduces BMLP as a general query answering problem using boolean matrices and presents two novel BMLP modules designed for efficient bottom-up inferences on linear and non-linear recursive datalog programs.
Related Work
Bottom-Up Datalog Evaluation
Historically, bottom-up datalog evaluation has relied on symbolic manipulations to compute the least model of graph-like datalog programs. Early works by Vieille (1986), Ceri, Gottlob, and Tanca (1989), and others have laid the foundation for these approaches. The concept of using boolean matrices for transitive closure computations dates back to Peirce (1932) and Copilowish (1948). Fischer and Meyer (1971) introduced a logarithmic divide-and-conquer technique that significantly improved computational efficiency.
Datalog Evaluation in Tensor Space
Several studies have explored the evaluation of first-order logic programs in tensor spaces. Grefenstette (2013) developed a tensor-based calculus for representing truth values of domain entities and logical relations. Nickel et al. (2011) and Rocktaschel et al. (2015) further extended these ideas to represent semantic webs and compute truth values using tensors. However, these approaches have limitations in handling recursive datalog programs.
First-Order Rule Learning with Tensors
Neural-symbolic methods have also been employed to approximate first-order datalog queries using tensors. Rocktaschel and Riedel (2017) and Yang, Yang, and Cohen (2017) used differentiable unification operators to construct neural networks for rule learning. Evans and Grefenstette (2018) introduced the δILP framework, which combines program templates with gradient descent in binary neural networks to optimize rule weights.
Research Methodology
Problem Definition
The BMLP problem is defined as follows: Given a datalog program containing a set of clauses with predicate symbols, the goal is to output a boolean matrix that encodes the least model of the program. This matrix representation allows for efficient boolean matrix operations to evaluate datalog queries.
Boolean Matrix Representation
A bijective function maps constants in a datalog program to a subset of natural numbers. This mapping enables the encoding of boolean matrices to represent clauses. Each row of the matrix corresponds to a fact, and the binary code of each row indicates the presence or absence of facts.
BMLP Modules
Two BMLP modules are introduced:
- Repeated Matrix Squaring (BMLP-RMS): This module computes the transitive closure of a boolean matrix using a logarithmic technique. It repeatedly squares the matrix product to avoid redundant computations.
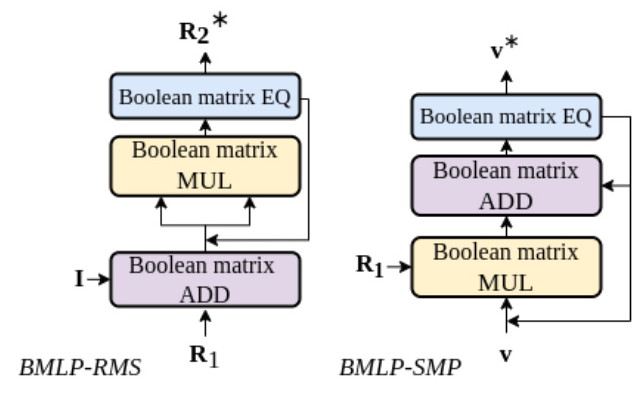
- Selective Matrix Product (BMLP-SMP): This module focuses on finding a specific subset of the least model for a partially grounded query. It uses vector multiplication to derive new facts iteratively.

Composability of BMLP Modules
The composability of BMLP modules is a key feature that allows for the evaluation of complex datalog programs. Linear BMLP modules can be combined to compute multilinear recursive datalog programs. This composability is theoretically proven based on the closed semiring of linear relational operators.
Experimental Design
Benchmarks
The experiments were conducted on synthetic benchmarks of directed graphs with cycles and the Freebase 15K dataset. The directed graph datasets were prepared for two tasks: all derivable groundings (DG) and partially grounded queries (DG+partial). The Freebase 15K dataset was used to evaluate the derivable facts for the isForeign predicate.
Compared Systems
The performance of BMLP modules was compared with state-of-the-art datalog engines (Souffle), general-purpose Prolog systems (SWI-Prolog and B-Prolog), and an Answer Set Programming (ASP) system (Clingo).
Preparation
The datasets were compiled into boolean matrices for BMLP modules. The experiments recorded the mean CPU time for evaluating various queries, with a runtime cap of 15000 seconds.
Results and Analysis
Performance Comparison
The results demonstrate that BMLP modules significantly outperform other systems in terms of runtime efficiency. For instance, BMLP-RMS is 9x faster than Souffle and 33x faster than B-Prolog when evaluating large programs with millions of facts.
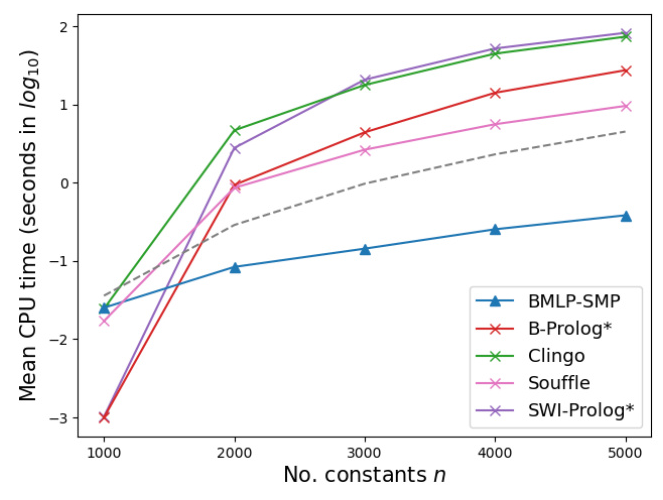
Runtime Analysis
The runtime of BMLP-RMS is not significantly affected by the number of facts in the program, supporting the theoretical time complexity of O(n^3 log2 n). BMLP-SMP shows a runtime growth slower than the cubic growth curve, aligning with its theoretical time complexity of O(n^3).
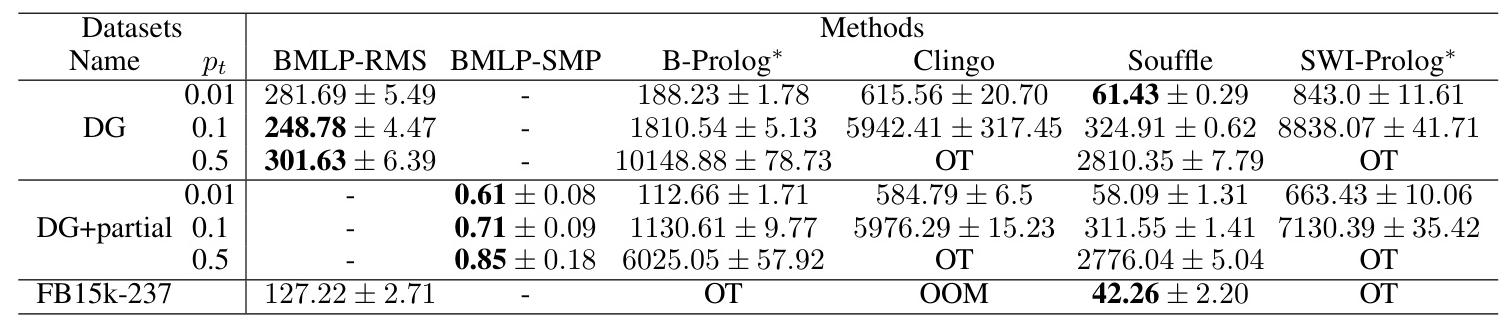
Efficiency on Sparse Matrices
While BMLP modules perform exceptionally well on dense matrices, their performance on sparse matrices is an area for future improvement.
Overall Conclusion
Boolean Matrix Logic Programming (BMLP) offers a powerful and efficient approach to datalog query evaluation. The introduction of BMLP-RMS and BMLP-SMP modules demonstrates significant performance improvements over traditional and state-of-the-art systems. The composability of BMLP modules allows for the evaluation of complex datalog programs, making BMLP a promising direction for future research in logic programming.
Future Work
Future work will focus on improving the performance of BMLP modules on sparse matrices and exploring the bilinearization framework for multilinear programs. Additionally, the potential of computing matrices on GPUs to further enhance query evaluation runtime will be investigated.
This blog post provides a comprehensive overview of the research on Boolean Matrix Logic Programming, highlighting its methodology, experimental design, and significant findings. The illustrations included help visualize the concepts and results discussed in the paper.

