Authors:
Róbert Csordás、Christopher Potts、Christopher D. Manning、Atticus Geiger
Paper:
https://arxiv.org/abs/2408.10920
Introduction
The Linear Representation Hypothesis (LRH) posits that neural networks encode concepts as linear directions in their activation space. This hypothesis has been a cornerstone in understanding neural network interpretability. However, the paper “Recurrent Neural Networks Learn to Store and Generate Sequences using Non-Linear Representations” by Róbert Csordás, Christopher Potts, Christopher D. Manning, and Atticus Geiger challenges this strong interpretation of the LRH. The authors present a counterexample demonstrating that gated recurrent neural networks (RNNs) can represent tokens using magnitudes rather than directions, leading to non-linear, layered representations termed “onion representations.”
Related Work
The Linear Representation Hypothesis
The LRH has been extensively studied, with early work on word vectors suggesting that linear operations on vectors can reveal meaningful structures. Recent studies have further articulated this hypothesis, emphasizing that features are represented as directions in vector space and are one-dimensional. However, some researchers have challenged the second point, showing that some features are irreducibly multi-dimensional. The strong form of the LRH asserts that all concepts are linearly encoded, a claim that this paper aims to refute.
Intervention-based Methods
Intervention-based methods have been pivotal in understanding neural network operations. These methods involve performing interventions on linear representations, such as entire vectors, individual dimensions, or linear subspaces. While these methods have provided significant insights, the space of non-linear representations remains underexplored.
Recurrent Neural Networks
RNNs, including LSTMs and GRUs, have been foundational in processing sequential data. Despite the rise of Transformer-based models, RNNs have regained attention with the development of structured state-space models. This study focuses on GRUs to understand their ability to store and generate sequences.
Research Methodology
The authors hypothesize that GRUs can store and generate sequences using non-linear representations. They test this hypothesis through a series of experiments involving the repeat task, where the network is trained to repeat an input sequence of tokens. The study explores three hypotheses:
- Unigram Variables: GRUs store each token in a linear subspace.
- Bigram Variables: GRUs store tuples of inputs (bigrams) in linear subspaces.
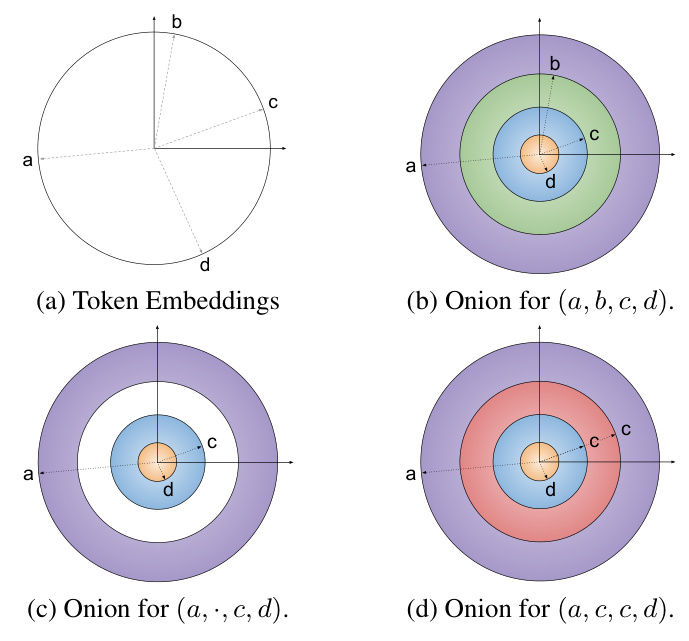
- Onion Representations: GRUs encode each position in a sequence as a magnitude, leading to layered, non-linear representations.
Experimental Design
Setup
The experiments involve generating 1 million random sequences for training and 5,000 sequences for testing. The maximum sequence length is 9, and the number of possible symbols is 30. The models are trained using GRU cells with varying hidden state sizes (48 to 1024). The training uses an AdamW optimizer with specific hyperparameters to ensure convergence.
Repeat Task Experiments
The repeat task involves presenting the network with a sequence of random tokens followed by a special token indicating the start of the repeat phase. The task is to repeat the input sequence. The performance of different GRU models on this task is evaluated to explore the core interpretability hypotheses.
Results and Analysis
Hypothesis 1: Unigram Variables
The authors use interchange interventions to determine if GRUs store each token in a separate linear subspace. The results show that larger models (N ≥ 512) successfully store each input element in different subspaces, while smaller models do not support this hypothesis.
Hypothesis 2: Bigram Variables
The second hypothesis posits that GRUs store bigram variables in linear subspaces. The results indicate that this hypothesis holds for most models except the smallest ones (N ≤ 64).
Hypothesis 3: Onion Representations
For the smallest models, the authors observe that the update gates of the GRUs close gradually, suggesting the use of magnitude-based encoding. The intervention experiments show that onion representations achieve significantly better accuracy for small models compared to linear unigram and bigram interventions.
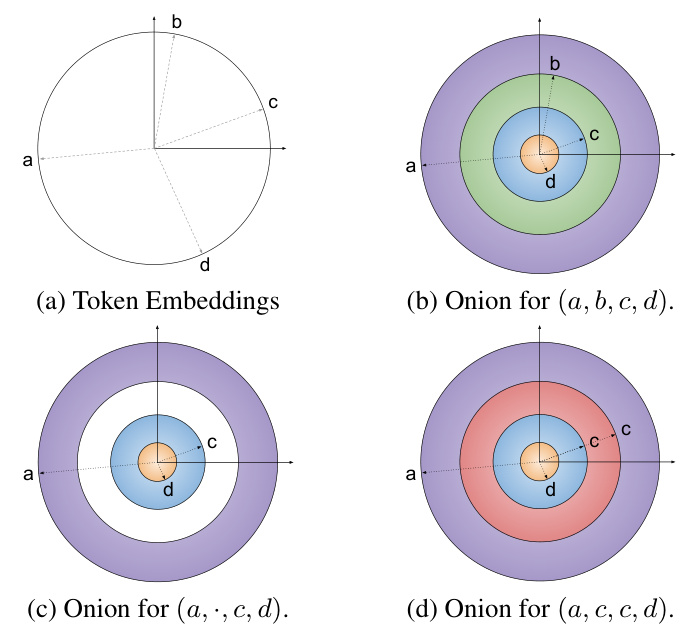
The visualizations of the input gates for different GRU models support the hypothesis that small models use onion representations, where the magnitude of the token embedding determines the position.

Overall Conclusion
The study presents a compelling counterexample to the strong form of the LRH, demonstrating that GRUs can use non-linear, magnitude-based representations to store and generate sequences. This finding challenges the prevailing focus on linear representations in interpretability research and suggests the need for broader exploration of non-linear mechanisms. The authors hope that this work will spur further research into non-linear representations and their implications for understanding neural network behavior.

Acknowledgements
The research was supported by a grant from Open Philanthropy, and Christopher D. Manning is a CIFAR Fellow.
This blog post provides a detailed interpretation of the paper “Recurrent Neural Networks Learn to Store and Generate Sequences using Non-Linear Representations,” highlighting the key findings and their implications for the field of neural network interpretability. The study’s counterexample to the strong LRH underscores the importance of considering non-linear representations in future research.