Authors:
Poppy Collis、Ryan Singh、Paul F Kinghorn、Christopher L Buckley
Paper:
https://arxiv.org/abs/2408.10970
Introduction
In the realm of artificial intelligence, one of the enduring challenges is the ability to flexibly learn discrete abstractions that are useful for solving inherently continuous problems. The human brain excels at distilling discrete concepts from continuous sensory data, enabling us to specify abstract sub-goals during planning and transfer this knowledge across new tasks. This capability is highly desirable in the design of autonomous systems. However, translating continuous problems into discrete space for decision-making remains a complex task.
This study explores the potential of recurrent switching linear dynamical systems (rSLDS) to provide useful abstractions for planning and control. By leveraging the rich representations formed by rSLDS, the authors propose a novel hierarchical model-based algorithm inspired by Active Inference. This algorithm integrates a discrete Markov Decision Process (MDP) with a low-level linear-quadratic controller, facilitating enhanced exploration and non-trivial planning through the delineation of abstract sub-goals.
Related Work
Hybrid models, particularly piecewise affine (PWA) systems, have been extensively studied and applied in real-world scenarios. Previous work by Abdulsamad et al. has utilized variants of rSLDS for optimal control of general nonlinear systems, focusing on value function approximation. In contrast, this study emphasizes online learning without expert data and flexible discrete planning.
The use of grid-based discretization for continuous spaces, while prevalent, becomes computationally expensive as dimensionality increases. This study seeks to address this by leveraging rSLDS to handle continuous variables while maintaining the benefits of decision-making in discrete domains.
Research Methodology
Framework Overview
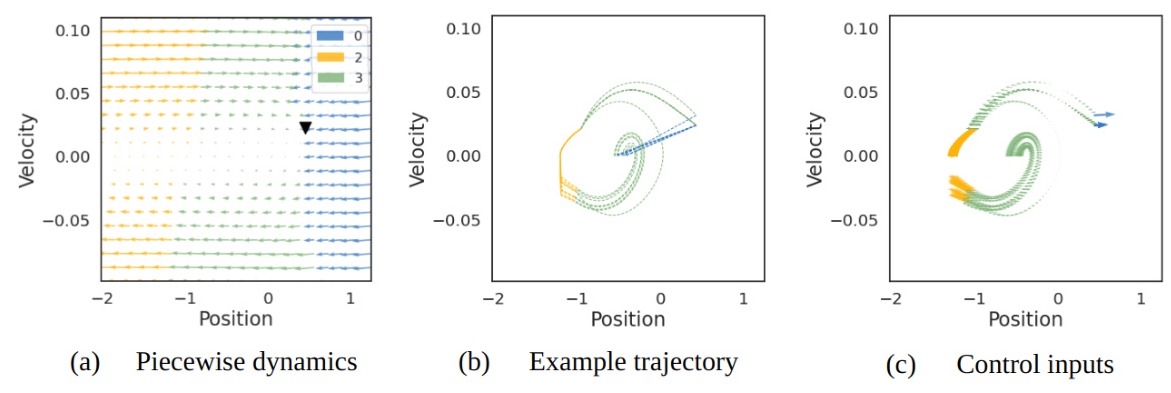
The proposed Hybrid Hierarchical Agent (HHA) algorithm decomposes nonlinear dynamics into piecewise affine regions of the state-space using an rSLDS. The recurrent generative model parameters of the rSLDS enable the identification of discrete regions within which goals reside, lifting goals into high-level objectives. The agent generates plans at a discrete level, specifying sequences of abstract sub-goals and driving the system into desired regions of the state-action space.
rSLDS (Recurrent-Only)
In the recurrent-only formulation of the rSLDS, discrete latent states are generated as a function of continuous latents and control inputs via a softmax regression model. The continuous dynamics evolve according to a discrete linear dynamical system indexed by the discrete latent states, with Gaussian diagonal noise. Bayesian updates are used to learn the rSLDS parameters, with approximate methods employed due to the non-Gaussian conditional likelihoods.
Discrete Planner
The discrete planner is modeled as a Bayesian Markov Decision Process (MDP), with states representing discrete latents found by the rSLDS. Actions correspond to the number of states, and state transition probabilities are parameterized with Dirichlet priors to facilitate directed exploration. The planner outputs discrete actions based on a receding horizon optimization, translating these actions into continuous control priors.
Continuous Controller
Continuous closed-loop control is managed by a finite-horizon linear-quadratic regulator (LQR) controller. The LQR controller minimizes a quadratic cost function, penalizing terminal state deviation and control input to ensure solutions remain within constraints. Approximate closed-loop solutions are computed offline, using parameters of the linear systems indexed by discrete modes and continuous control priors.
Experimental Design
Task and Initialization
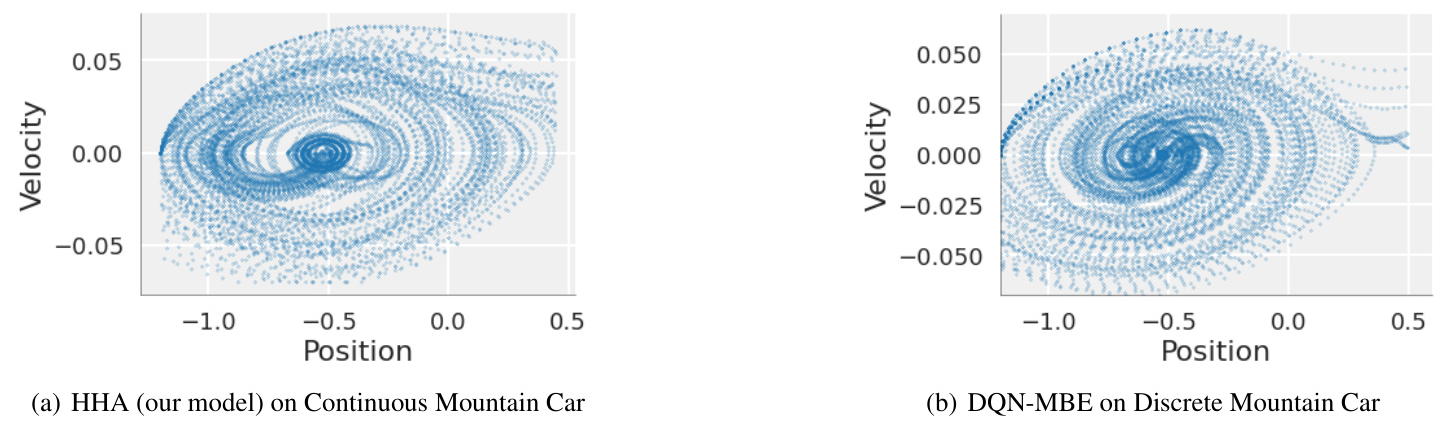
The performance of the HHA model was evaluated using the Continuous Mountain Car task, a classic control problem characterized by sparse rewards. The HHA was initialized following the procedure outlined by Linderman et al. (2016), with rSLDS parameters fitted to observed trajectories every 1000 steps unless a reward threshold was reached within a single episode.
Evaluation Metrics
The evaluation focused on the ability of the HHA to find piecewise affine approximations of the task-space, perform comprehensive exploration, and achieve successful planning and control. Comparisons were made with other reinforcement learning baselines, including Actor-Critic and Soft Actor-Critic models.
Results and Analysis
Piecewise Affine Approximations
The HHA effectively found piecewise affine approximations of the task-space, using discrete modes to solve the task. The rSLDS divided the space according to position, velocity, and control input, with useful modes identified in the position space. Once the goal and system approximation were established, the HHA consistently navigated to the reward.
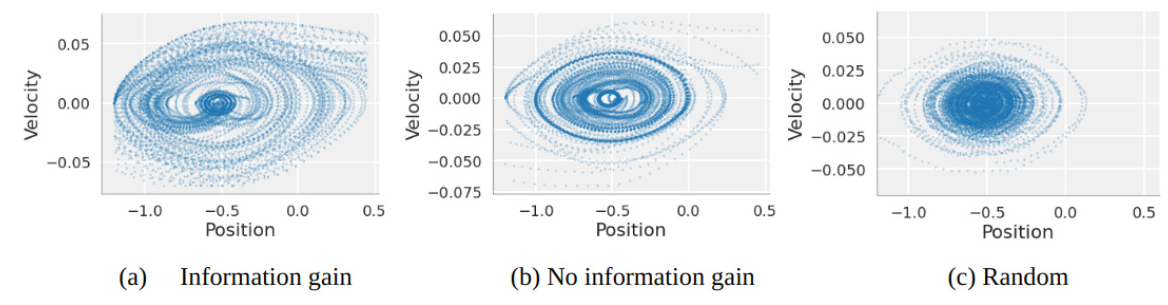
Exploration and State-Space Coverage
The HHA demonstrated comprehensive exploration of the state-space, with significant gains observed when using information-gain drive in policy selection. Even without information-gain, the HHA outperformed random action control due to the non-grid discretization of the state-space, reducing the dimensionality of the search space in a behaviorally relevant manner.
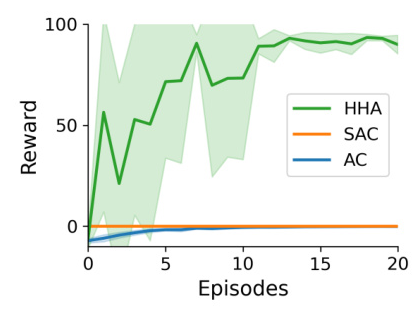
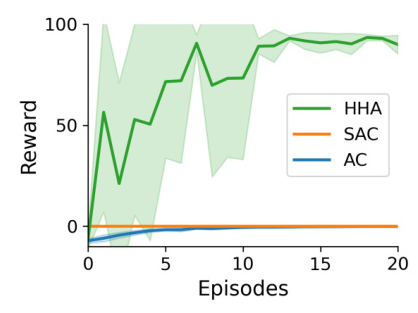
Performance Comparison
The HHA outperformed other reinforcement learning baselines, finding the reward and capitalizing on its experience significantly quicker. The model’s performance was comparable to model-based algorithms with exploratory enhancements in the discrete Mountain Car task.
Overall Conclusion
The study demonstrates that rSLDS representations hold promise for enriching planning and control in continuous domains. The emergence of non-grid discretizations allows for fast system identification and successful planning through abstract sub-goals. While some loss of optimality may occur compared to black-box approximators, the approach eases online computational burden and maintains functional simplicity and interpretability.
Future work may explore better solutions for handling control input constraints and align the method with control-theoretic approaches to ensure robust system performance and reliability. The findings contribute to advancing the field of machine learning, particularly in the context of hierarchical planning and control.