Authors:

Muhammad Najib、Giuseppe Perelli

Paper:

https://arxiv.org/abs/2408.10074

Synthesis of Reward Machines for Multi-Agent Equilibrium Design: An Interpretive Blog

Introduction

In the realm of game theory, mechanism design has long been a cornerstone for crafting games that yield desired outcomes. However, a nuanced yet distinct concept known as equilibrium design has emerged, where the designer’s authority is more constrained. Instead of creating games from scratch, the designer modifies existing incentive structures to achieve specific outcomes. This paper delves into equilibrium design using dynamic incentive structures called reward machines. The study employs weighted concurrent game structures with mean-payoff objectives to model the game and explores how reward machines can dynamically allocate rewards to optimize the designer’s goals. The primary focus is on the payoff improvement problem, which examines whether a dynamic incentive can enhance the designer’s payoff beyond a certain threshold. The paper presents two variants of this problem—strong and weak—and demonstrates that both can be solved in polynomial time using a Turing machine equipped with an NP oracle.

Related Work

This study builds on a rich foundation of game-theoretic research, particularly in the analysis of concurrent and multi-agent systems using Nash equilibrium (NE) and other concepts. Previous works have modeled systems as games where agents act rationally to fulfill their preferences, often expressed through mean-payoff objectives. The game-theoretical analysis of mean-payoff games (MPGs) has been pivotal in verifying their correctness. Equilibrium design, inspired by mechanism design, offers a way to rectify equilibrium outcomes without creating the game from scratch. Previous research has explored subsidy schemes to introduce equilibria in concurrent MPGs satisfying certain logical formulas. This paper generalizes the incentive model using reward machines, which dynamically assign rewards based on the execution history, offering a more expressive model of incentives.

Research Methodology

Mean-Payoff and Multi-Player Mean-Payoff Games

The study begins by defining the mean-payoff value for infinite sequences and multi-player mean-payoff games. A multi-player mean-payoff game is characterized by a set of players, actions, states, and transition functions, with each player having a weight function over the states. The global weight function measures the designer’s satisfaction, also as a mean-payoff value over executions.

Reward Machines

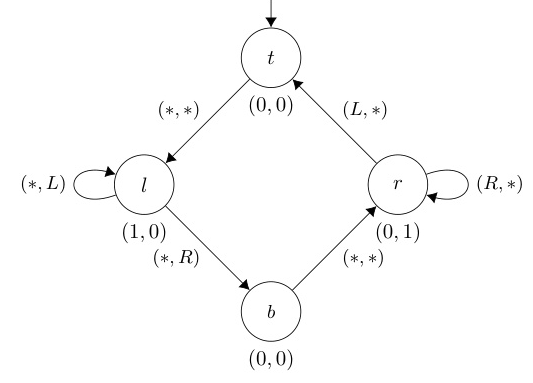
Reward machines are introduced as finite state machines that dynamically assign rewards based on the execution history. Formally, a reward machine is defined as a Mealy machine, which takes a path as input and outputs a sequence of reward vectors for the players at each step of the path. The implementation of a reward machine on a game involves modifying the game’s transition and weight functions to incorporate the rewards assigned by the machine.

Improvement Problems

The paper defines two main decision problems within the framework: the global payoff weak improvement problem and the global payoff strong improvement problem. These problems ask whether there exists a reward machine that can improve the designer’s payoff by more than a given threshold value. The study also considers approximate solutions, aiming to find a reward machine that can improve the global payoff by a value ε-close to the desired threshold.

Experimental Design

Auxiliary Game Construction

To solve the improvement problems, the study constructs an auxiliary game that treats reward machines as strategies for a designated agent. This auxiliary game allows the problem to be viewed as an equilibrium verification problem. The construction involves adding an agent to the original game, whose actions represent the possible rewards assigned to other agents. The auxiliary game’s states are augmented to record the rewards received by each agent, and the global weight function is updated accordingly.

Strategy Translation

The study presents constructions to translate reward machines into strategies for the auxiliary game and vice versa. These constructions ensure that the paths and outcomes of the original game and the auxiliary game correspond correctly, preserving the payoffs of agents.

Results and Analysis

Solving Improvement Problems

The study introduces a technique for solving the weak and strong improvement problems by computing the worst and best Nash Equilibria (NE) for both the original and auxiliary games. The NE threshold problem is used as a subroutine to determine whether there exists an NE with payoffs falling between two vectors. The study provides algorithms for computing approximate values of worstNE and bestNE, ensuring termination by computing ε-approximations.

Complexity Analysis

The paper demonstrates that the problems of computing ε-bestNE and ε-worstNE for both the original and auxiliary games are FPNP-complete. It also shows that the strong and weak ε-improvement problems are ∆P2-complete, with the strong problem being NP-hard and the weak problem being coNP-hard.

Synthesis of Reward Machines

If the improvement problem returns a positive answer, the corresponding reward machine can be synthesized by finding a strategy profile in the auxiliary game that achieves the desired payoff improvement. The reward machine is then constructed from this strategy profile.

Overall Conclusion

This paper explores the use of reward machines to enhance designer satisfaction in multi-agent mean-payoff games. By dynamically assigning rewards based on execution history, reward machines offer a more expressive model of incentives compared to subsidy schemes. The study addresses the global payoff improvement problem, presenting algorithms to solve it and demonstrating the complexity of the problem. The findings highlight the potential of reward machines in equilibrium design, offering a complementary approach to norm-based equilibrium design.

Future Work

Future research could explore extensions of designers’ and agents’ objectives, such as combining LTL and mean-payoff objectives or employing multi-valued logic for rational verification. Additionally, integrating reward machines with normative systems could provide a balanced approach between obligation and recommendation modalities, enhancing the effectiveness of equilibrium design.

Illustrations:

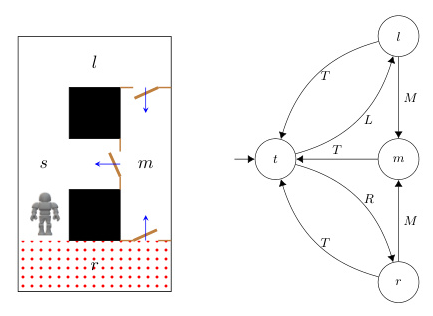
• Example scenario with a robot navigating an environment with four locations:
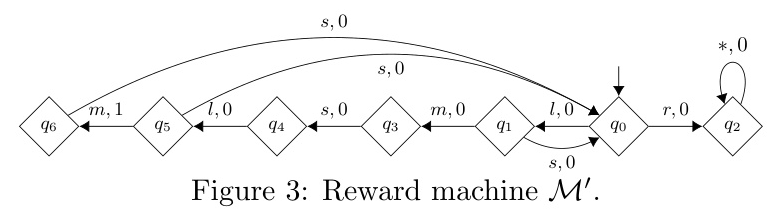
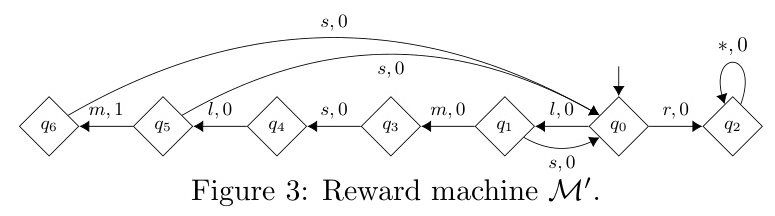
• Reward machine for the example scenario:
• Game arena representation: