Authors:
Yucheng Sheng、Kai Huang、Le Liang、Peng Liu、Shi Jin、Geoffrey Ye Li
Paper:
https://arxiv.org/abs/2408.08707
Introduction
Millimeter-wave (mmWave) communication is a cornerstone technology for next-generation wireless networks due to its vast bandwidth capabilities. However, mmWave signals suffer from significant path loss, necessitating the use of extensive antenna arrays and frequent beam training to ensure optimal directional transmission. Traditional deep learning models, such as long short-term memory (LSTM) networks, have been employed to enhance beam tracking accuracy. Despite their effectiveness, these models often struggle with robustness and generalization across different wireless environments.
In this study, we propose leveraging large language models (LLMs) to improve the robustness of beam prediction. By converting time series data into text-based representations and employing the Prompt-as-Prefix (PaP) technique for contextual enrichment, our approach harnesses the strengths of LLMs for time series forecasting. Simulation results demonstrate that our LLM-based method offers superior robustness and generalization compared to LSTM-based models, showcasing the potential of LLMs in wireless communications.
System Model
We consider a downlink mmWave transmission scenario for a single user, where the base station (BS) and user terminals (UTs) are equipped with multiple antennas. The well-known Saleh-Valenzuela (SV) channel model is adopted to accurately model the beam variations resulting from UT mobility. The channel vector for the n-th time slot is expressed as:
[ h_n = \sum_{l=1}^{L_n} \sqrt{\frac{1}{\rho_{n,l}}} \alpha_{n,l} a^*(\phi_{n,l}) ]
where ( L_n ) denotes the number of paths, ( \rho_{n,l} ) is the path loss, ( \alpha_{n,l} ) is the complex gain, and ( \phi_{n,l} ) is the angle of departure (AoD). The antenna response vector ( a(\phi) ) is defined for a uniform linear array (ULA) as:
[ a(\phi) = \left[ 1, e^{j2\pi d \sin \phi / \lambda}, \ldots, e^{j\pi(M-1)d \sin \phi / \lambda} \right]^T ]
The beam prediction task aims to forecast the transmit beam with the largest gain from a discrete Fourier transform (DFT) codebook of candidate beams. The optimal beam index ( q^* ) is determined by:
[ q^* = \arg \max_{q \in {0,1,2,\ldots,Q-1}} \left| h^T f^{(q)} \right|^2 ]
Our goal is to predict the optimal beam for the next H time steps based on past T time steps, maximizing the normalized beamforming gain.
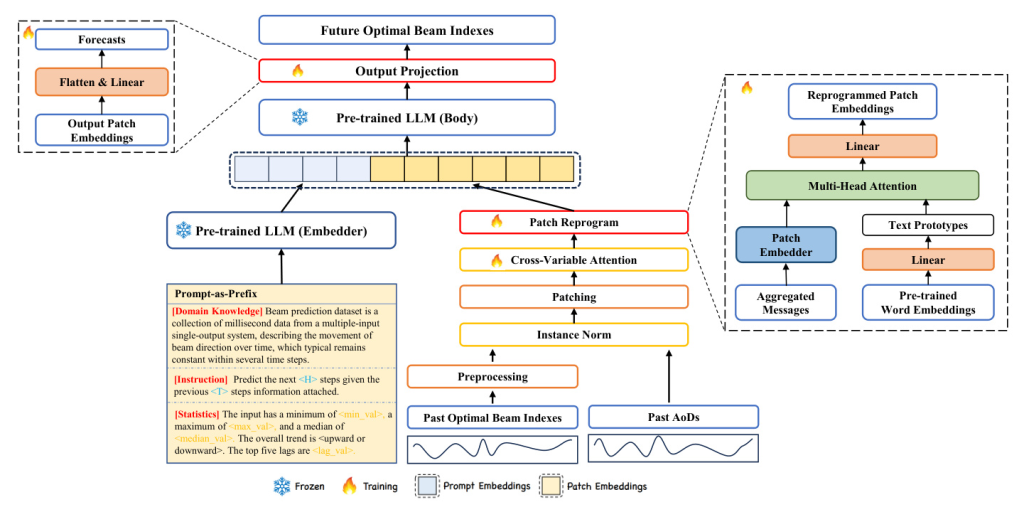
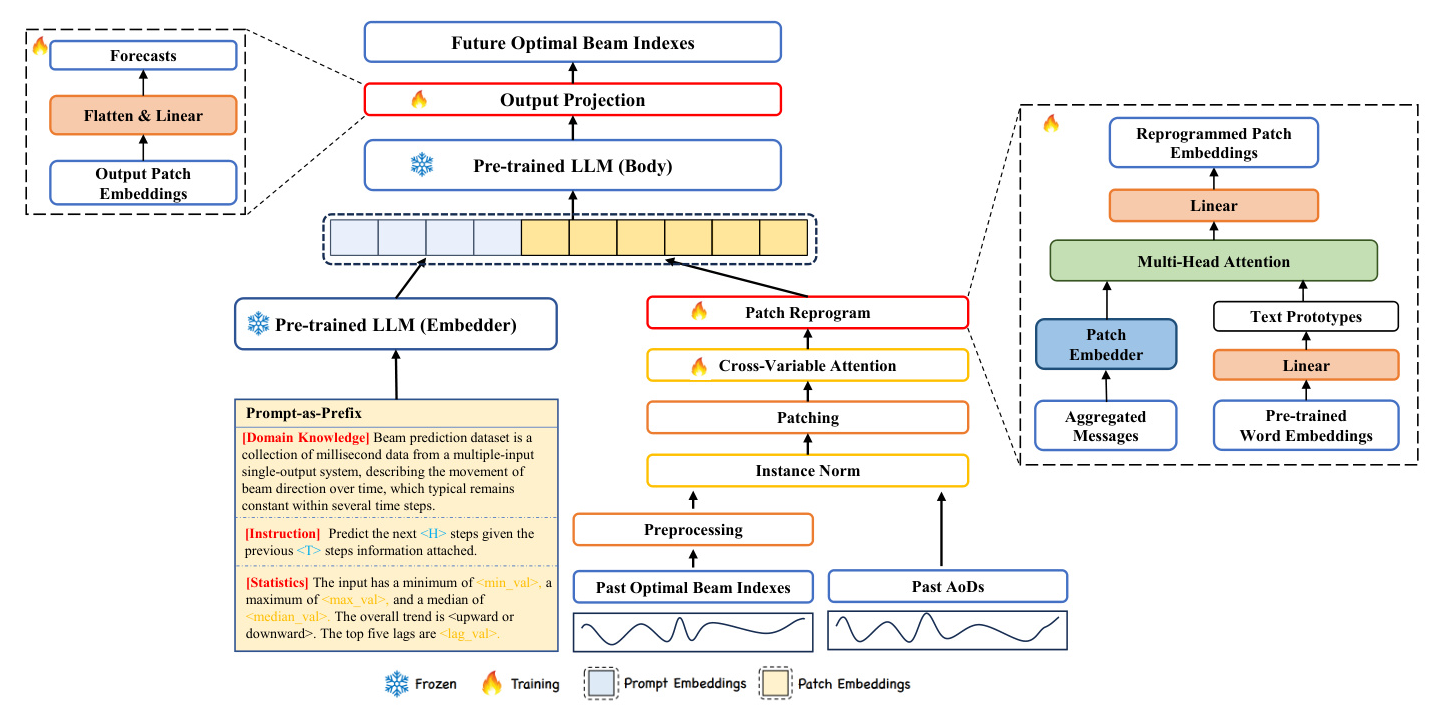
Prediction Model Based on LLM
Input Preprocessing
We use past optimal beam indexes and AoDs as historical observations. To enhance generalization, we map the sequence of past optimal beam indexes into the angular domain and ensure continuity between values at consecutive time steps. The input is then normalized using reversible instance normalization (RevIN) and segmented into patches.
Input Embedding
Each input sample is normalized and segmented into patches, which are then embedded using a linear layer. This process preserves local semantic information and reduces computational complexity.
Cross-Variable Attention
A learnable vector is used as a router to aggregate messages from all variables through cross-variable attention. This step analyzes the relationship between the optimal beam indexes and AoDs, aggregating messages into a compact representation.
Patch Reprogramming
We reprogram patch embeddings into the source data representation space to align the modalities of time series and natural language. This involves using pre-trained word embeddings and a multi-head cross-attention layer to adaptively select relevant source information.
Prompt-as-Prefix
Prompting is used to activate the LLM for task-specific reasoning. We incorporate domain knowledge, instructions, and statistical summaries as prefixes in the prompts, significantly improving the LLM’s adaptability to downstream tasks.
Output Projection
The output representations from the LLM are flattened and linearly projected to derive the final forecasts. The loss function minimizes the mean-squared errors between the ground truths and predictions of the optimal beam indexes.
Simulation
Simulation System Setup
We select GPT-2 as our backbone model and compare our method with two LSTM-based methods: ODE and CascadedLSTM. The DeepMIMO dataset is used for training and validation, focusing on an outdoor environment to reflect real-world conditions. The BSs are configured with different numbers of antennas, and the beam prediction period is set to 16 ms.
Simulation Results
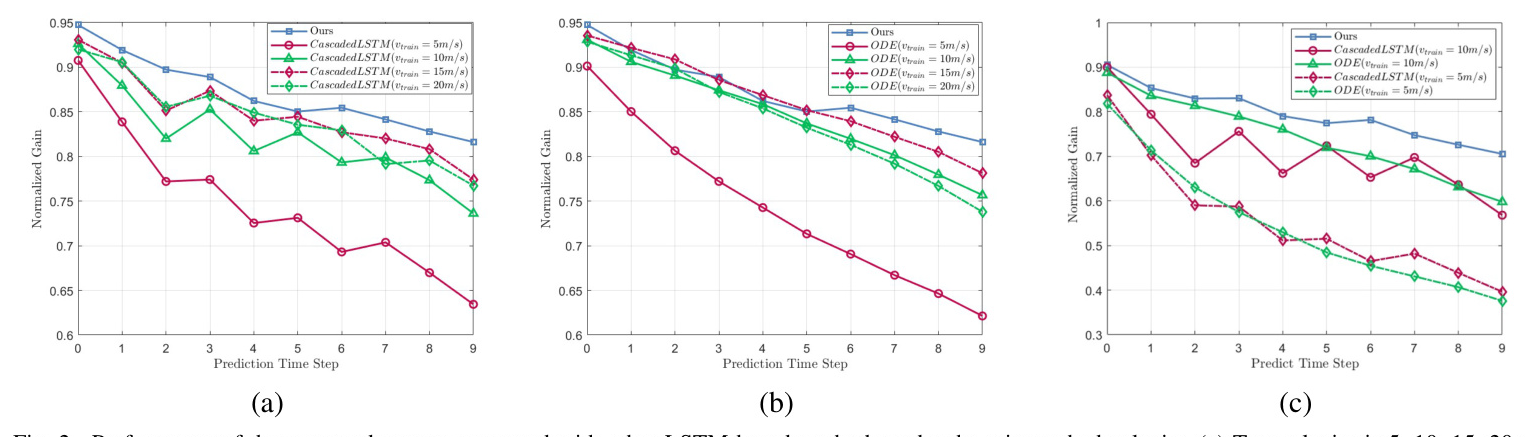
Robustness Across Different Speeds
Our model’s performance is evaluated across various speeds. The results show that our LLM-based method outperforms LSTM-based methods, particularly at mismatched speeds. This highlights the improved robustness of large models trained at various speeds.
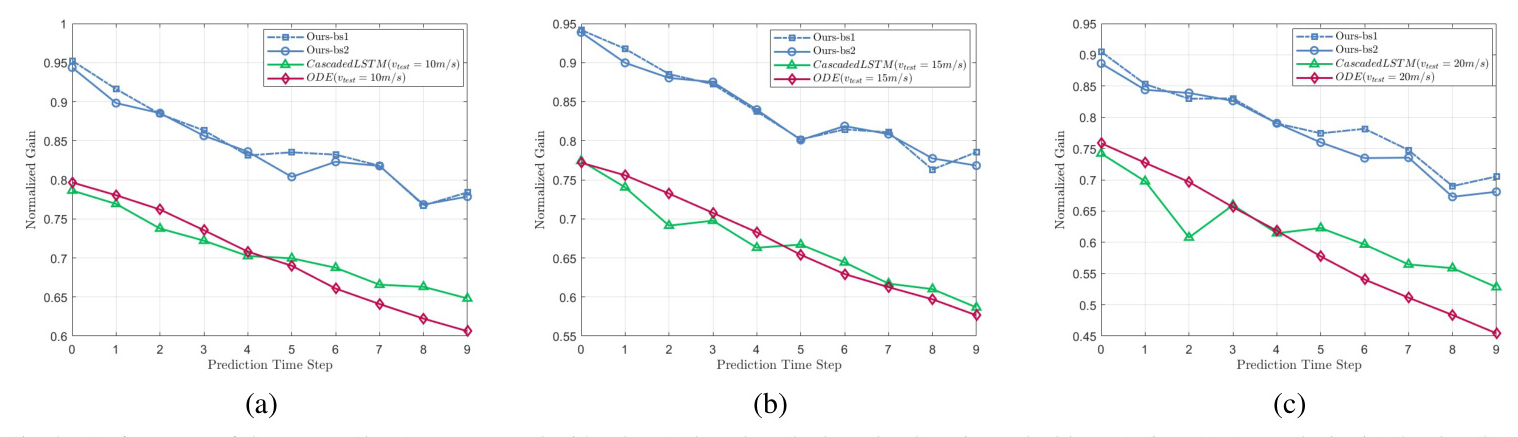
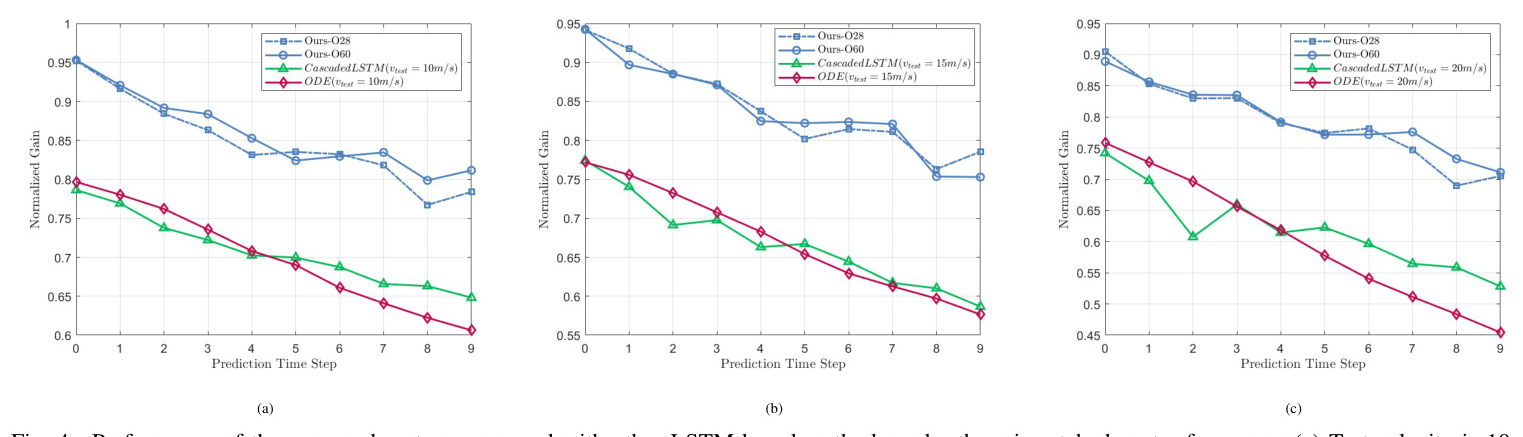
Robustness Across Different Base Stations
We test our model’s robustness across different BSs. The LSTM-based models show significant performance deterioration when tested on different BSs, while our LLM-based solution maintains strong performance, demonstrating the powerful zero-shot learning capabilities of LLMs.
Robustness Across Different Center Frequencies
Our LLM-based solution shows remarkable robustness when tested at different center frequencies. This robustness is attributed to our input setup, which is less dependent on channel characteristics compared to LSTM-based methods.
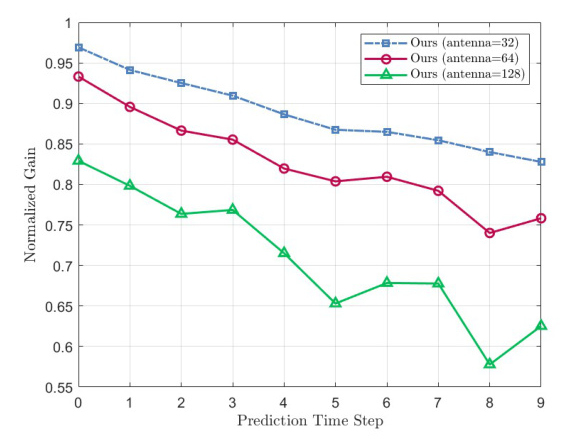
Performance with Different Antenna Configurations
Our solution functions effectively across different antenna configurations, unlike LSTM-based solutions that require redesign and retraining. The overall normalized gain increases as the number of antennas decreases, due to the narrowing beamwidth with more antennas.

Ablation Experiment
An ablation experiment demonstrates the necessity of including external variables. Using both the optimal beam and AoD as inputs significantly improves performance compared to using only the optimal beam.
Conclusion
We have presented a novel framework that adapts LLMs for beam prediction in wireless communications. By aggregating optimal beam indexes and AoDs and converting them into text-based prototype representations, we align the data format with LLM capabilities. Our innovative PaP technique further enhances the model’s understanding and reasoning of wireless data. This work marks the first integration of LLMs with wireless transmission, suggesting significant potential for diverse applications in wireless communications.