Authors:
Victor Verreet、Lennert De Smet、Luc De Raedt、Emanuele Sansone
Paper:
https://arxiv.org/abs/2408.08133
Introduction
The field of neuro-symbolic (NeSy) artificial intelligence (AI) aims to combine the perceptive capabilities of neural networks with the reasoning capabilities of symbolic systems. Neural probabilistic logic systems follow this paradigm by integrating neural networks with probabilistic logic. This combination allows for better generalization, handling of uncertainty, and reduced training data requirements compared to pure neural networks. However, the main challenge lies in learning, as the learning signal for the neural network must propagate through the probabilistic logic component.
Existing methods for propagating the learning signal include exact propagation using knowledge compilation, which scales poorly for complex systems, and various approximation schemes that introduce biases or require extensive optimization. To address these issues, this research proposes a surrogate objective to approximate the data likelihood, providing strong statistical guarantees. The EXPLAIN, AGREE, LEARN (EXAL) method is introduced to construct this surrogate objective, enabling scalable learning for more complex systems.
Background
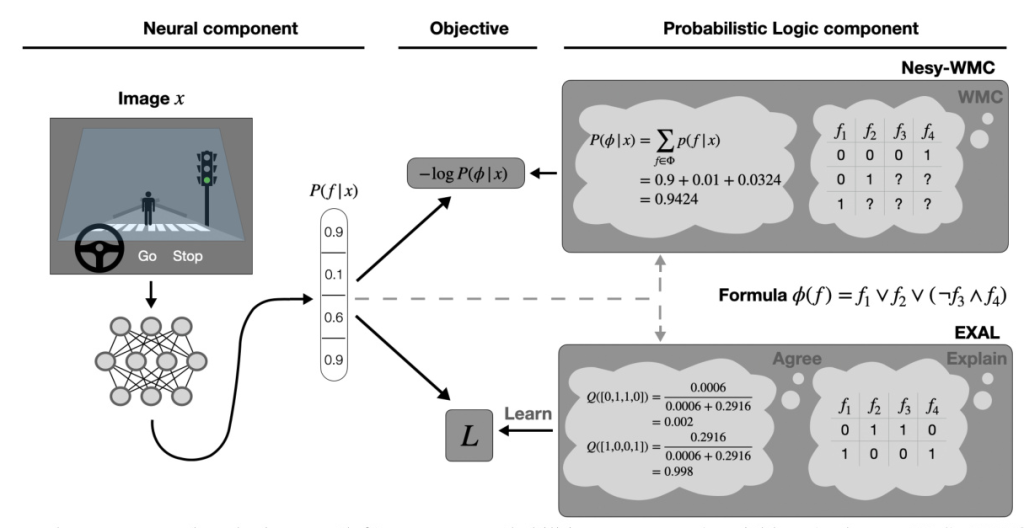
NeSy systems consist of both a neural and a symbolic component. The neural component handles perception by mapping raw input to a probability distribution over binary variables. The symbolic component performs logical reasoning over these variables to verify whether a formula is satisfied. Weighted model counting (WMC) is chosen for the symbolic component, as probabilistic inference can be reduced to WMC.
Definitions
- Assignment: An assignment of binary variables, which can be partial or complete.
- Explanation: A complete assignment that satisfies a formula.
- WMC Problem: Defined by a propositional logical formula and weight assignments for each variable. The answer to the WMC problem is the sum of the weights of all explanations that satisfy the formula.
- NeSy-WMC Problem: A WMC problem where the weights are computed by a neural network.
Example
Consider a self-driving car that must decide whether to brake based on an image. The neural component outputs probabilities for detecting a pedestrian, red light, driving slow, and crosswalk. The logical component decides the car should brake if there is a pedestrian, a red light, or if it is driving too fast near a crosswalk. This is encoded in a formula, and the weights are given by the neural component. The answer to the NeSy-WMC problem is the probability that the car should brake given the input image.
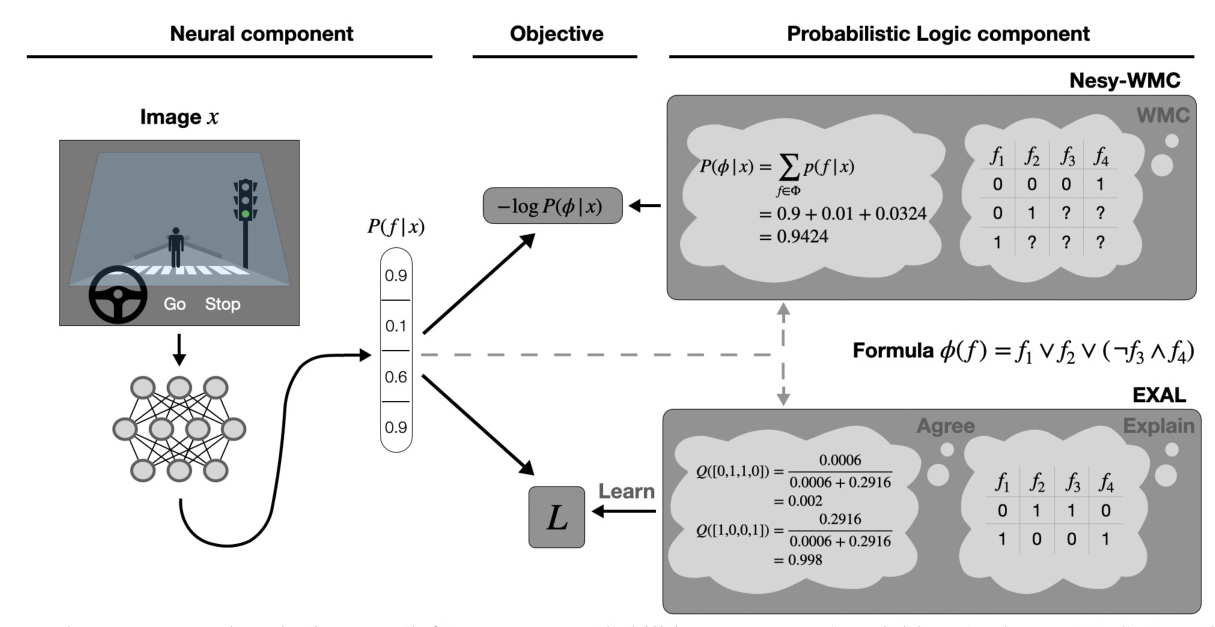
The Objective
The objective is to optimize a NeSy-WMC model consisting of a neural and logic component. The data set contains tuples of raw input and logical formulas. The setup is modeled by a probabilistic graphical model, where the neural component outputs a distribution over binary variables, and the logic component is deterministic.
Surrogate Objective
To avoid expensive inference, a surrogate objective is proposed that bounds the true likelihood. The surrogate objective is defined as the Kullback-Leibler (KL) divergence between auxiliary distributions over explanations and the distributions output by the neural component. The tightest bound is obtained by minimizing the KL divergence with respect to both distributions.

EXPLAIN, AGREE, LEARN
The EXAL method aims to minimize the surrogate objective by constructing a suitable proposal distribution for learning.
EXPLAIN: Sampling Explanations
The EXPLAIN algorithm samples explanations of the logical formula using a stochastic variant of the Davis–Putnam–Logemann–Loveland (DPLL) algorithm. The sampling strategy determines the distribution of returned explanations.
AGREE: Updating the Weights
The AGREE step reweights the sampled explanations based on the neural component’s output. The optimal weights are proportional to the neural component’s output, minimizing the surrogate objective.
LEARN: Updating the Neural Component
The LEARN step minimizes the surrogate objective with respect to the neural component’s parameters using standard gradient descent techniques. The full EXAL algorithm is shown in Algorithm 2.
Optimizations using Diversity
To improve the surrogate objective, the concept of diversity is introduced. Sampling a diverse set of explanations increases the chance of seeing the true explanation, leading to a tighter bound on the negative log-likelihood.
Diversity of Explanations
Diversity is defined as the number of unique explanations sampled. Increasing diversity leads to a tighter bound on the surrogate objective.
Reformulation as a Markov Decision Process
The execution of EXPLAIN can be framed as a Markov decision process (MDP), allowing the use of generative flow networks (GFlowNets) to optimize the sampling strategy for increased diversity.
Experiments
Experiments validate the theoretical claims and demonstrate the effectiveness of EXAL on the MNIST addition and Warcraft pathfinding tasks.
Diversity (EXPLAIN)
Different sampling strategies are compared in terms of diversity. The results show that increasing the diversity parameter improves the diversity of sampled explanations.
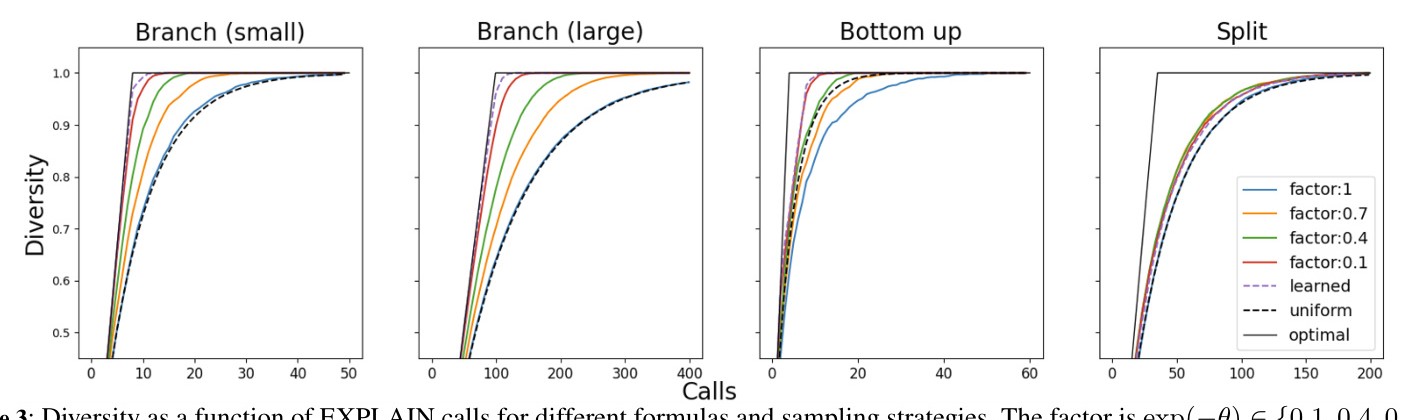
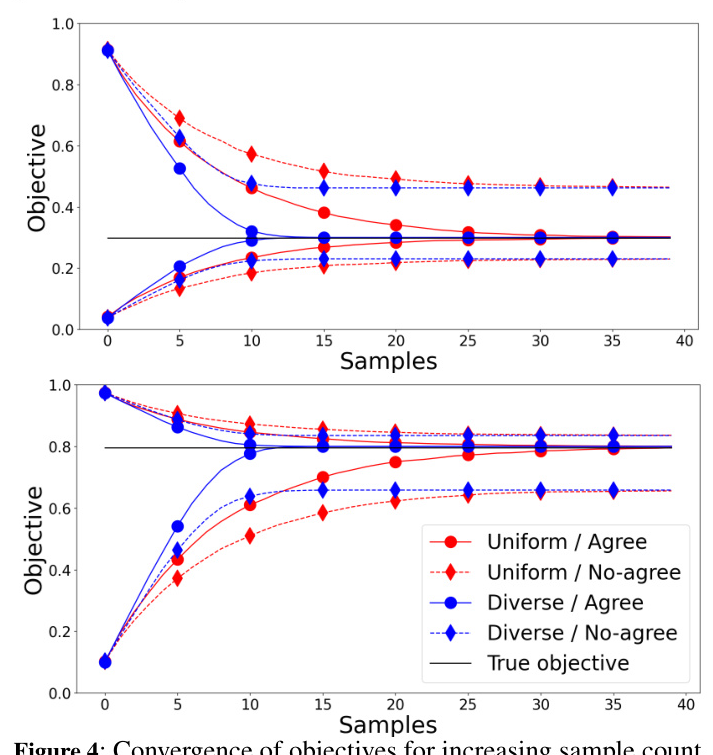
Convergence of Bounds (AGREE)
The importance of diversity and the AGREE step is demonstrated by comparing the surrogate objective with the true likelihood for different sample counts. The results confirm that diversity improves the error bounds.
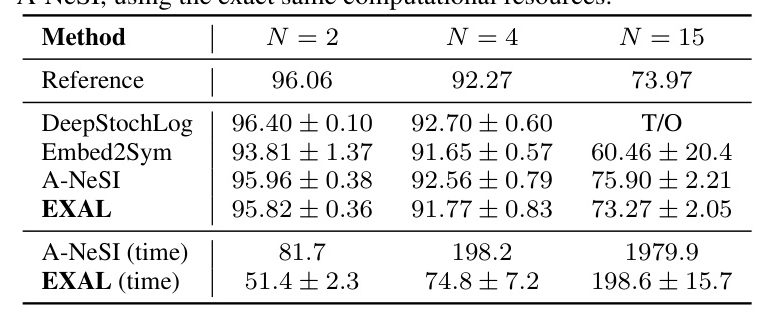
MNIST Addition (EXAL)
EXAL is evaluated on the task of learning to sum MNIST digits. The results show that EXAL is competitive with state-of-the-art methods in terms of accuracy and significantly outperforms them in terms of speed.
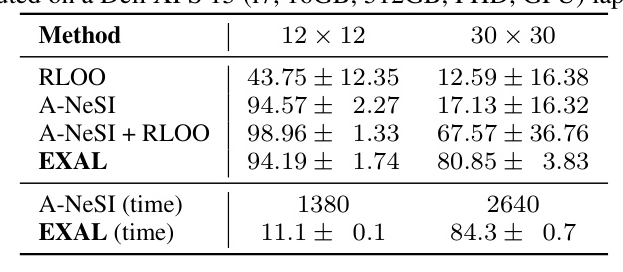
Warcraft Pathfinding (EXAL)
EXAL is applied to the Warcraft pathfinding task, demonstrating faster learning times and higher accuracy compared to state-of-the-art methods.
Related Work
Recent works on NeSy learning and scalable logical inference are reviewed. The proposed method differs from existing approaches by avoiding continuous relaxations and iterative optimization methods, instead leveraging explanation sampling for scalable learning.
Discussion and Conclusion
The EXAL method provides a scalable solution for learning in neural probabilistic logic systems. By using explanation sampling, the learning signal can be propagated through the symbolic component efficiently. Theoretical guarantees on the approximation error and practical methods to reduce this error are provided. Experimentally, EXAL is shown to be competitive with state-of-the-art methods in terms of accuracy and significantly faster in terms of learning time. Future work includes addressing reasoning shortcuts, scaling structure learning, and extending EXAL to support continuous variables in the symbolic representation.