Authors:
Lachlan McGinness、Peter Baumgartner
Paper:
https://arxiv.org/abs/2408.07854
Machine learning (ML) has revolutionized the way we solve problems and automate tasks. However, the interpretability of ML models remains a significant challenge. In this blog, we delve into a novel approach called CON-FOLD, an extension of the FOLD-RM algorithm, which introduces confidence scores to enhance the explainability of ML models.
Introduction
Machine learning models, while powerful, often lack transparency. Decision trees are an exception, providing a clear set of rules for decision-making. The FOLD (First Order Learner of Default) algorithm, introduced by Shakerin et al., generates interpretable rules but can sometimes be misleading. For instance, a rule derived from the Titanic dataset might suggest that all female passengers without a third-class ticket survived, which is not always true. To address this, CON-FOLD extends FOLD-RM by assigning confidence scores to each rule, indicating the reliability of predictions.
Formal Framework and Background
CON-FOLD operates within the logic programming framework. A rule in this context is a logical statement that defines a relationship between features and outcomes. The learning algorithm takes positive and negative training examples and generates rules that classify data points into target classes. The confidence scores are calculated using the Wilson Score Interval, which adjusts for small sample sizes and extreme probabilities, making the model more trustworthy.

Related Work
Confidence scores have been used in decision tree learning to assess pruning steps. Decision trees can be expressed as sets of production rules, which can be simplified using scoring functions. The FOLD family of algorithms stands out by using default negation to handle exceptions, leading to more concise rule sets compared to traditional decision tree classifiers.
The CON-FOLD Algorithm and Confidence Scores
The CON-FOLD algorithm assigns confidence scores to rules as they are created. These scores are derived from the Wilson Score Interval, ensuring they are reliable even with small amounts of data. The algorithm follows a structured process to generate rules and calculate confidence scores, as illustrated in Algorithm 1.
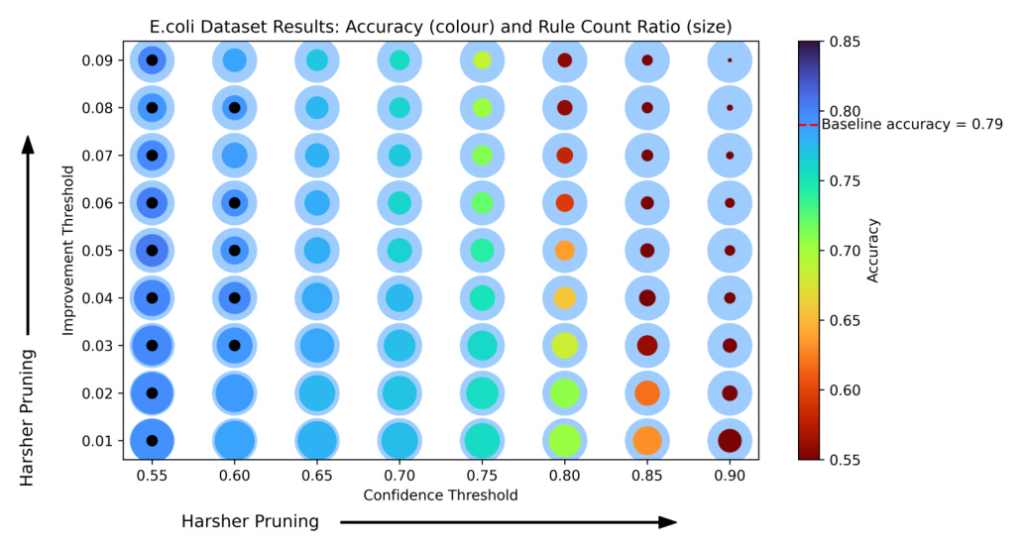
Improvement Threshold Pruning
To prevent overfitting, CON-FOLD employs improvement threshold pruning. This method evaluates each rule and its exceptions, removing those that do not significantly improve the confidence score. The process is formalized in Algorithm 2.
Confidence Threshold Pruning
In addition to reducing rule depth, confidence threshold pruning removes rules with low confidence scores. This ensures that only reliable rules are retained, simplifying the model and enhancing interpretability.
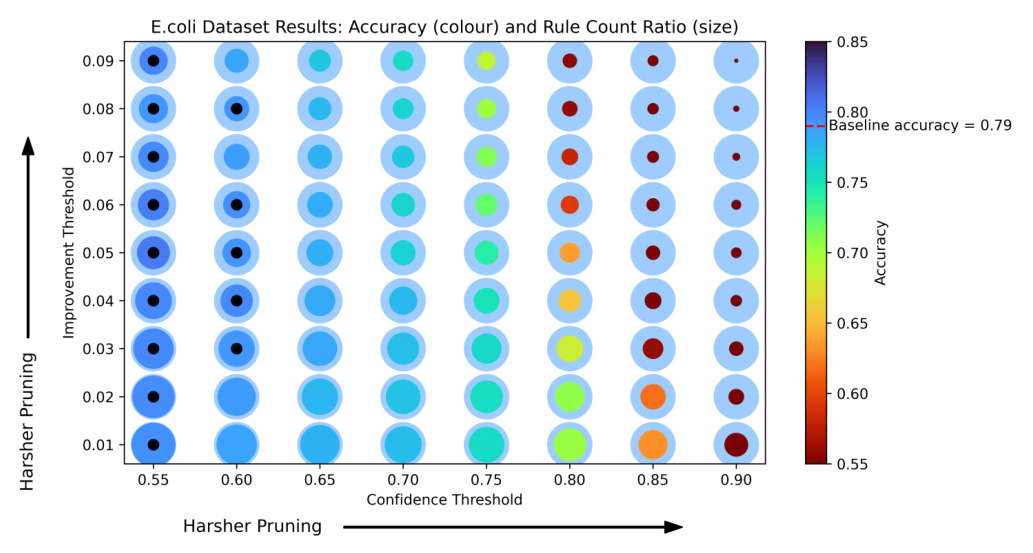
Inverse Brier Score
To evaluate the performance of probabilistic predictions, CON-FOLD introduces the Inverse Brier Score (IBS). This metric rewards accurate predictions with high confidence and penalizes incorrect high-confidence predictions. IBS is a proper scoring system that aligns with traditional accuracy metrics, making it suitable for comparing probabilistic and non-probabilistic models.
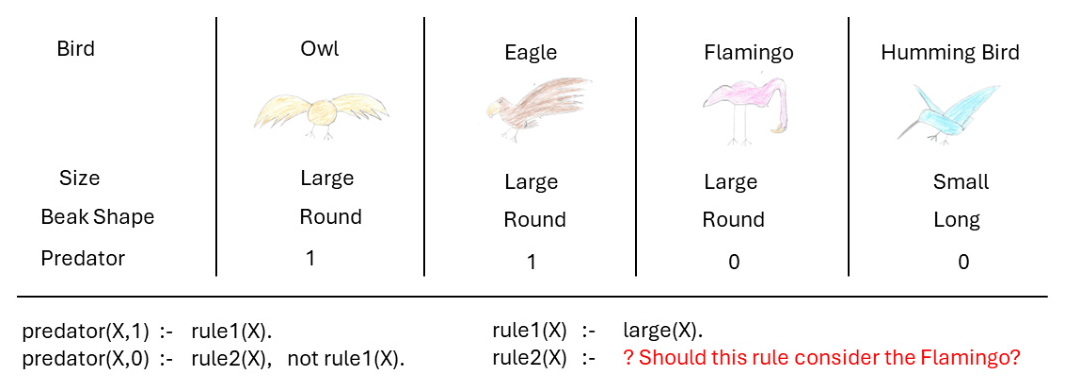
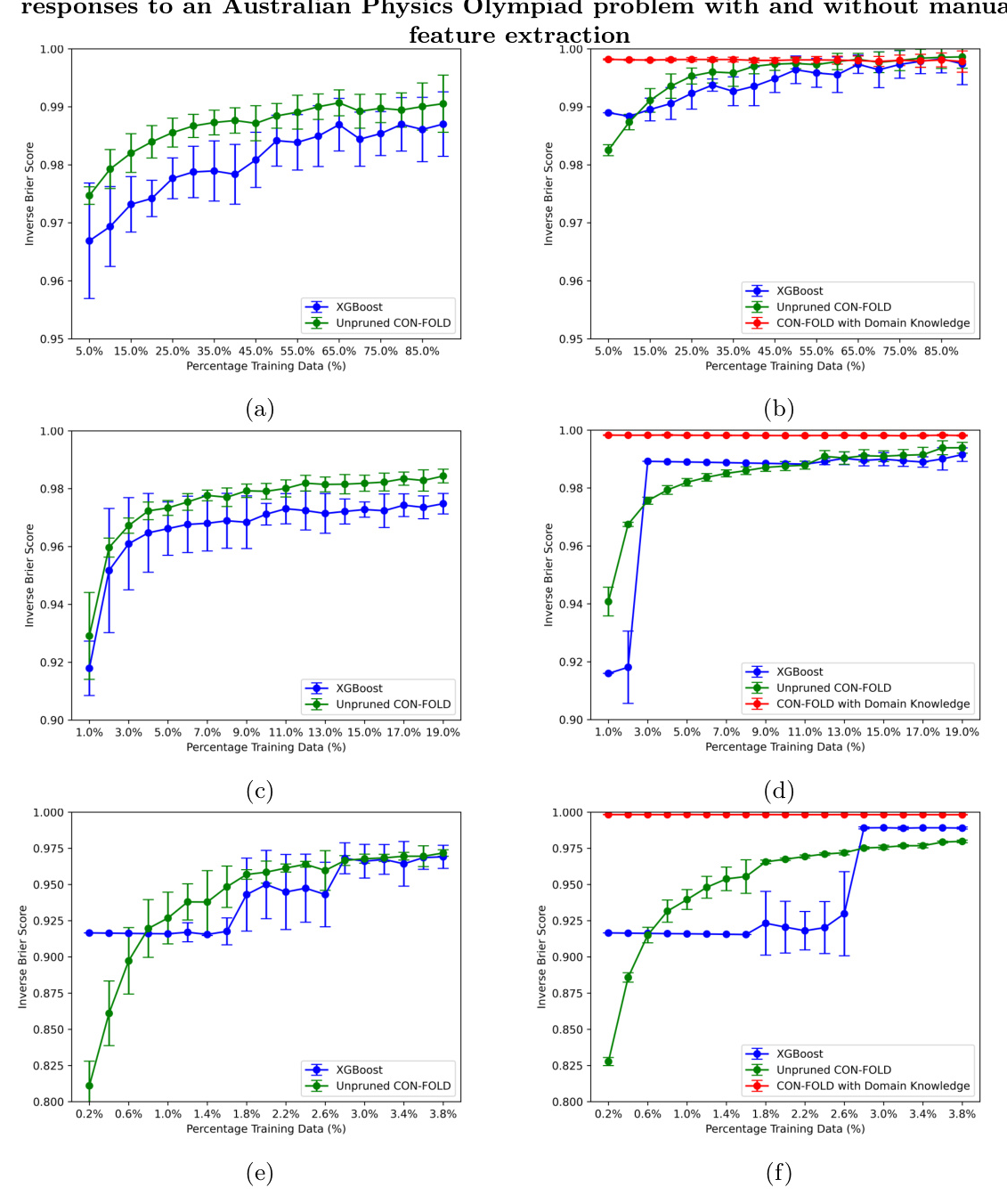
Manual Addition of Rules and Physics Marking
One of the key advantages of FOLD is the ability to incorporate background knowledge in the form of rules. This is particularly useful in domains with limited training data, such as grading student responses to physics problems. By adding domain-specific rules, CON-FOLD can significantly improve performance, as demonstrated with data from the Australian Physics Olympiad.
Results
CON-FOLD was evaluated against XGBoost, FOLD-RM, and FOLD-SE using datasets from the UCI Machine Learning Repository. The results, summarized in Table 1, show that CON-FOLD with pruning reduces the number of rules while maintaining high accuracy. The inclusion of confidence scores gives CON-FOLD an edge, especially with small training datasets.
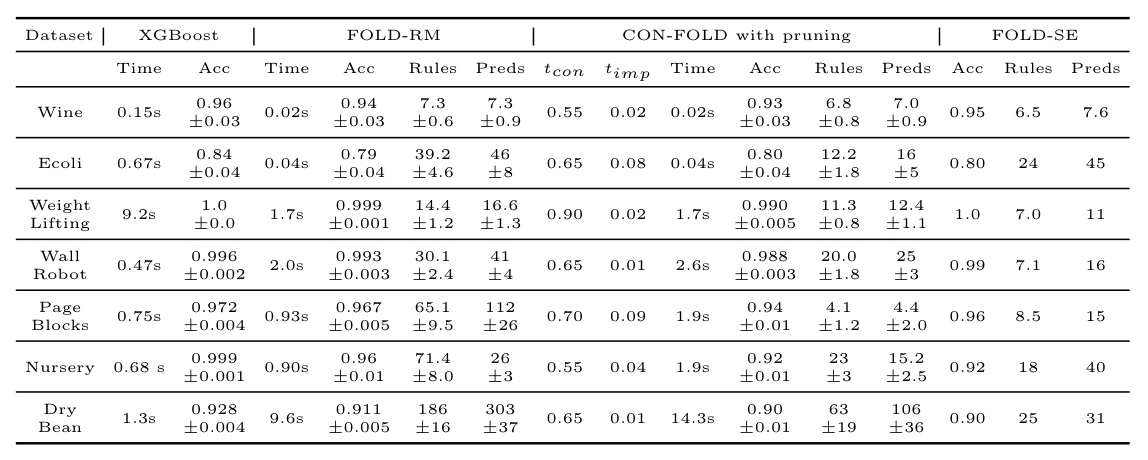
Discussion
The results highlight the scalability and efficiency of CON-FOLD. The pruning algorithm effectively reduces the number of rules, making the model more interpretable. The ability to include background knowledge further enhances the model’s performance, particularly in domains with limited training data.
Conclusion and Future Work
CON-FOLD introduces confidence values to the FOLD algorithm, enhancing the interpretability and reliability of ML models. The pruning algorithm reduces rule complexity, and the Inverse Brier Score provides a robust metric for evaluating probabilistic predictions. Future work could explore advanced feature extraction techniques and the integration of large language models to further improve the model’s capabilities.
Acknowledgements
The authors thank Australian Science Innovations for providing data from the 2023 Australian Physics Olympiad. This research was supported by a scholarship from CSIRO’s Data61. The ethical aspects of this research have been approved by the ANU Human Research Ethics Committee. All code can be accessed on GitHub at GitHub Repository.
This blog provides a comprehensive overview of the CON-FOLD algorithm, highlighting its innovations and practical applications. By introducing confidence scores and effective pruning methods, CON-FOLD enhances the explainability and reliability of machine learning models.