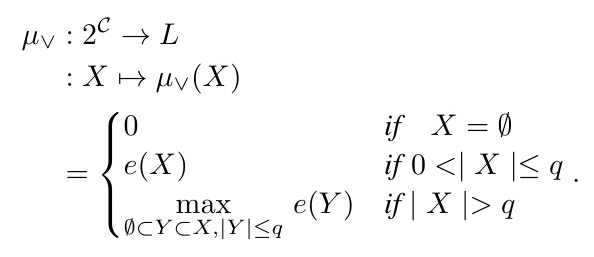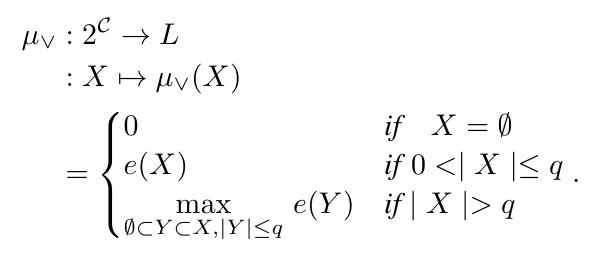Authors:
Paper:
https://arxiv.org/abs/2408.07768
On Learning Capacities of Sugeno Integrals with Systems of Fuzzy Relational Equations
Introduction
In decision theory, the Sugeno integral is a widely used qualitative aggregation function. It relies on a set function called capacity, which models the importance or interaction of subsets of criteria. This integral finds applications in various fields such as uncertainty modeling, multicriteria aggregation, and game theory. Recent approaches have aimed to learn the capacity of a Sugeno integral based on training data. This paper introduces a method for learning such capacities using systems of fuzzy relational equations.
Background
Sugeno Integral
The Sugeno integral framework includes:
– A set of criteria ( C = {1, 2, …, n} ).
– An evaluation scale ( L = { \xi_1 = 0, \xi_2, …, \xi_l = 1 } ) or ( L = [0, 1] ).
– A capacity ( \mu: 2^C \rightarrow L ) that satisfies ( \mu(\emptyset) = 0 ), ( \mu(C) = 1 ), and ( A \subseteq B \Rightarrow \mu(A) \leq \mu(B) ).
The Sugeno integral is given by two equivalent formulas:
[ S_\mu(x) = \max_{A \in 2^C} \min \left( \min_{i \in A} x_i, \mu(A) \right) ]
[ S_\mu(x) = \min_{A \in 2^C} \max \left( \max_{i \in A} x_i, \mu(A) \right) ]
Solving Systems of Max-Min and Min-Max Fuzzy Relational Equations
A system of max-min fuzzy relational equations is defined as:
[ A \boxdot_{\max \min} x = b ]
where ( A ) is a matrix, ( b ) is a vector, and ( x ) is the unknown vector. The greatest solution can be found using the G\”odel implication.
Similarly, a system of min-max fuzzy relational equations is defined as:
[ \Gamma \boxdot_{\min \max} x = \beta ]
where ( \Gamma ) is a matrix, ( \beta ) is a vector, and ( x ) is the unknown vector. The lowest solution can be found using the epsilon product.
Learning Capacities for Sugeno Integrals According to Data with Systems of Fuzzy Relational Equations
Constructing Two Systems of Fuzzy Relational Equations from Training Data
Given a set of ( N ) training data items ((x^{(k)}, \alpha^{(k)})), we construct two matrices ( M ) and ( \Gamma ), and a vector ( \alpha ):
– ( M = [m_{k,A}] ) where ( m_{k,A} = \min_{i \in A} x^{(k)}i )
– ( \Gamma = [\gamma{k,A}] ) where ( \gamma_{k,A} = \max_{i \in A} x^{(k)}_i )
– ( \alpha = [\alpha^{(k)}] )
We then form the following systems:
[ M \boxdot_{\max \min} X = \alpha ]
[ \Gamma \boxdot_{\min \max} X = \alpha ]
Preliminary Results
The potential extremal solutions ( e ) and ( f ) of the systems are increasing set functions. We define:
[ \mu_e(A) = \begin{cases}
e(A) & \text{if } A \neq \emptyset \
0 & \text{if } A = \emptyset
\end{cases} ]
[ \mu_f(A) = \begin{cases}
f(A) & \text{if } A \subset C \
1 & \text{if } A = C
\end{cases} ]
Learning Capacities
To ensure that ( \mu_e ) and ( \mu_f ) are capacities compatible with the training data, the systems must be consistent, and ( \mu_e(C) = 1 ) and ( \mu_f(\emptyset) = 0 ). Theorem 1 establishes the equivalence of these conditions with the existence of a capacity representing the training data.
Constructing q-Maxitive and q-Minitive Capacities
For a given training data item, we provide sufficient conditions for the existence of q-maxitive and q-minitive capacities. These capacities reduce the complexity of computing the global evaluation of an object by considering fewer subsets of criteria.
Example
Consider ( n = 3 ) criteria and the following training data:
– ( x^{(1)} = (0.15, 0.2, 0.3) ), ( \alpha^{(1)} = 0.2 )
– ( x^{(2)} = (0.5, 0.25, 0.3) ), ( \alpha^{(2)} = 0.3 )
– ( x^{(3)} = (0.4, 0.7, 0.35) ), ( \alpha^{(3)} = 0.4 )
We construct the system ( M \boxdot_{\max \min} X = \alpha ) and find the greatest solution, which represents the data as a 2-maxitive capacity.

Learning q-Maxitive/Minutive Capacities in Practice
In practice, we restrict learning to subsets of criteria with cardinality less than or equal to ( q ). We define the system:
[ M_q \boxdot_{\max \min} X = \alpha ]
where ( M_q ) is a reduced matrix. Theorem 2 and Theorem 3 provide conditions for the existence of q-maxitive and q-minitive capacities, respectively.
Learning Approximate Capacities
When dealing with real data, systems may become inconsistent. We use the Chebyshev distance to handle inconsistencies and obtain approximate solutions. Propositions 3 and 4 provide methods for constructing the greatest approximate q-maxitive and q-minitive capacities.
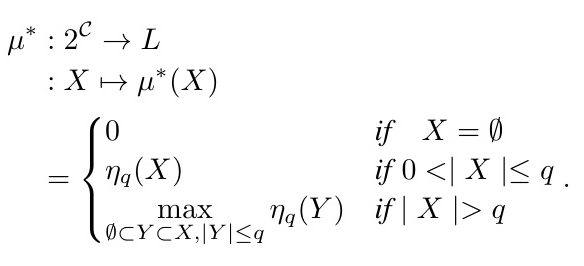
Conclusion
This paper introduces a method for learning capacities of Sugeno integrals based on systems of fuzzy relational equations. The approach can learn approximate q-maxitive and q-minitive capacities. Future work includes exploring the relationship between inconsistent systems and testing the method on real data.