Authors:
Jinseong Park、Seungyun Lee、Woojin Jeong、Yujin Choi、Jaewook Lee
Paper:
https://arxiv.org/abs/2408.06672
Introduction
Time series generation is a crucial task in various real-world applications such as simulation, data augmentation, and hypothesis testing. Traditional methods like variational autoencoders (VAE) and generative adversarial networks (GANs) have been widely used, but diffusion models have recently emerged as a powerful alternative. These models are known for their ability to generate high-quality and diverse time series data. However, standard Gaussian priors used in these models may not be suitable for time series data due to their unique characteristics like fixed time order and data scaling.
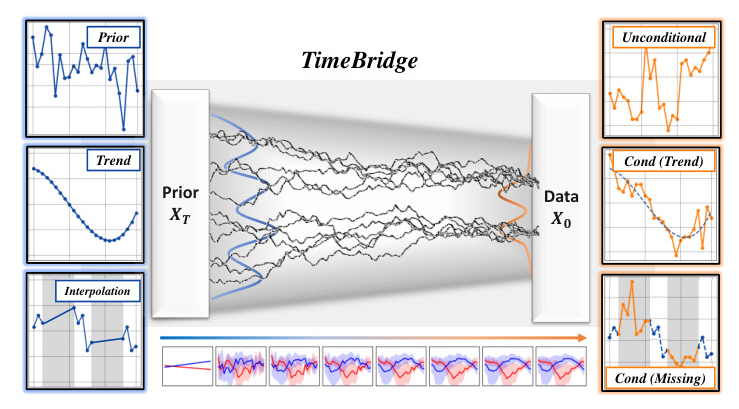
In this paper, the authors propose TimeBridge, a framework that leverages diffusion bridges to learn the transport between chosen prior and data distributions. This approach allows for flexible synthesis by using diverse prior distributions tailored to time series data.
Preliminaries
Diffusion Process
The diffusion process in standard models involves gradually injecting noise into samples drawn from the data distribution, forwarding them into a standard Gaussian distribution. This process is governed by a stochastic differential equation (SDE):
[ d\mathbf{x}_t = f(\mathbf{x}_t, t)dt + g(t)d\mathbf{w}_t ]
where ( f ) is the drift function, ( g ) is the diffusion coefficient, and ( \mathbf{w}_t ) is the Wiener process. The reverse SDE is formulated to estimate the reverse trajectory.
Diffusion Bridge
Standard diffusion models are limited by their inflexibility in choosing a prior distribution. The diffusion bridge extends this by allowing the construction of the diffusion process towards any endpoint using Doob’s h-transform. This approach is particularly useful for conditional tasks like image-to-image translation and text-to-speech synthesis.
Problem Statement
The paper addresses two types of time series synthesis tasks: unconditional and conditional generation. Unconditional generation aims to mimic the input dataset, while conditional generation uses paired conditions to guide the synthesis. The authors investigate the effectiveness of different prior distributions for these tasks through the following research questions:
- Are data-dependent priors effective for time series?
- How to model temporal dynamics with priors?
- Can constraints be used as priors for diffusion?
- How to preserve data points with diffusion bridge?
Diffusion Prior Design with TimeBridge
Data- and Time-dependent Priors for Time Series
Data-Dependent Prior
For unconditional tasks, the authors suggest using data-dependent priors to better approximate the data distribution. This involves setting the prior distribution as:
[ \mathbf{x}_T \sim \mathcal{N}(\mu, \text{diag}(\sigma^2)) ]
where ( \mu ) and ( \sigma^2 ) are calculated independently in the same dimension as the time series.
Time-Dependent Prior
To capture temporal dependencies, the authors employ Gaussian processes (GPs) for prior selection. The GP prior is defined as:
[ \mathbf{x}_T \sim \text{GP}(m, K + \Sigma) ]
where ( K ) is the kernel function and ( \Sigma ) is a correlation matrix function.
Scale-preserving Sampling for Conditional Priors
Soft Constraints with Given Trends
For trend-guided generation, the diffusion bridge sets the prior as the condition, allowing the model to learn the correction starting from the trend samples.
Hard Constraints with Fixed Points
For tasks requiring fixed points, the authors introduce a point-preserving sampling method that prevents adding noise to the values to be fixed. This method is particularly useful for imputation tasks.
TimeBridge: Bridge Modeling for Time Series
TimeBridge leverages the flexibility of prior selection as a diffusion bridge designed for time series. The model uses a Fourier-based loss function and transformer encoder-decoder models with seasonal-trend decomposition. The objective function is formulated as:
[ L_\theta = \mathbb{E}{t, x_0}[w_t(\|\mathbf{x}_0 – D\theta(\mathbf{x}t, t, \mathbf{x}_T)\|^2 + \lambda\|\text{FFT}(\mathbf{x}_0) – \text{FFT}(D\theta(\mathbf{x}_t, t, \mathbf{x}_T))\|^2)] ]
where ( w_t ) is the weight scheduler and ( \lambda ) is the strength of the fast Fourier transform (FFT).
Related Works
The paper discusses various standard diffusion models for time series and existing time series bridge models. It highlights the limitations of these models and the need for a more flexible framework like TimeBridge.
Experiments
Experimental Setup
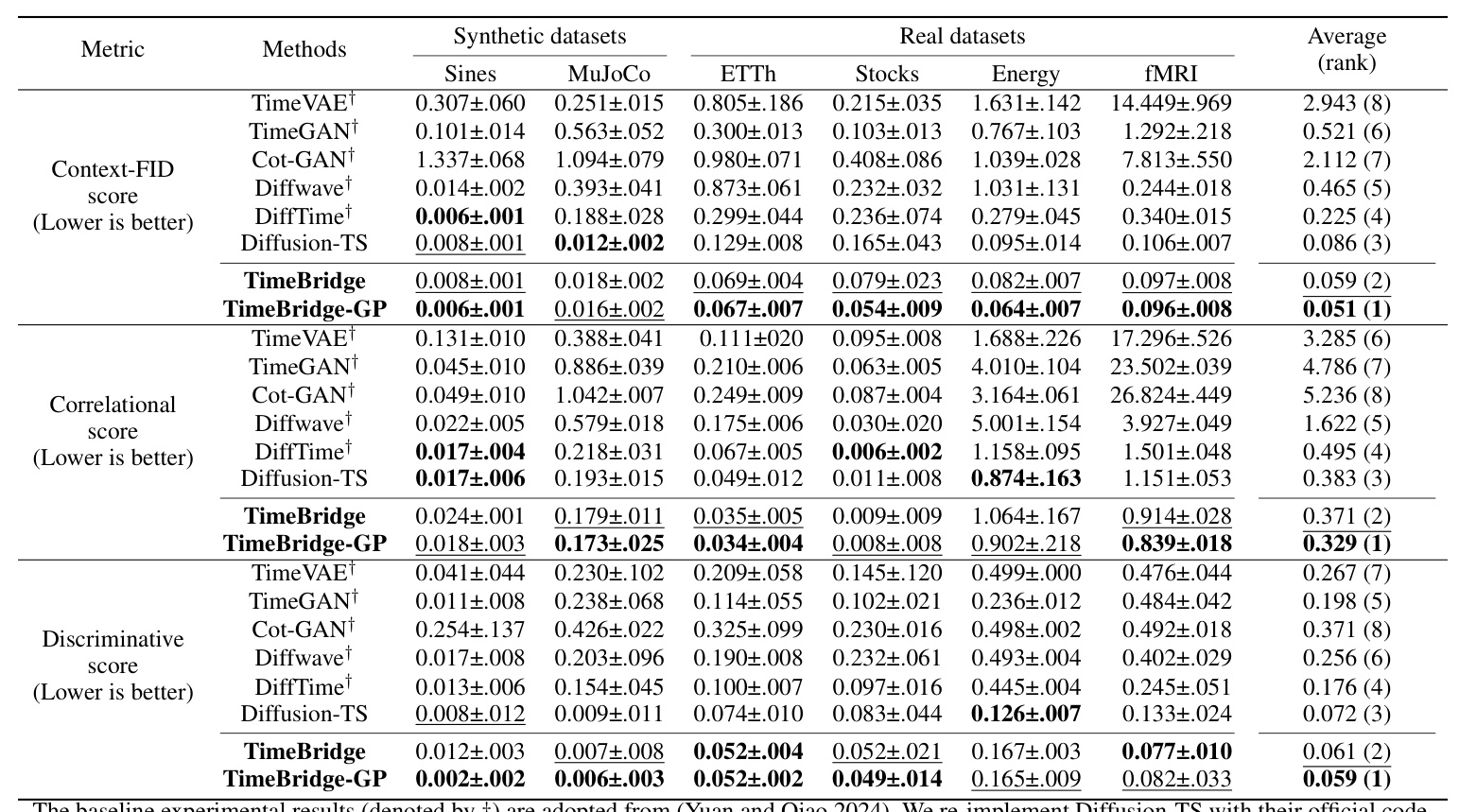
The authors assess the performance of TimeBridge using widely used time series datasets, including synthetic datasets (Sines, MuJoCo) and real-world datasets (ETT, Stocks, Energy, fMRI). They evaluate the models using metrics like Context-FID score, correlational score, and discriminative score.
Unconditional Generation
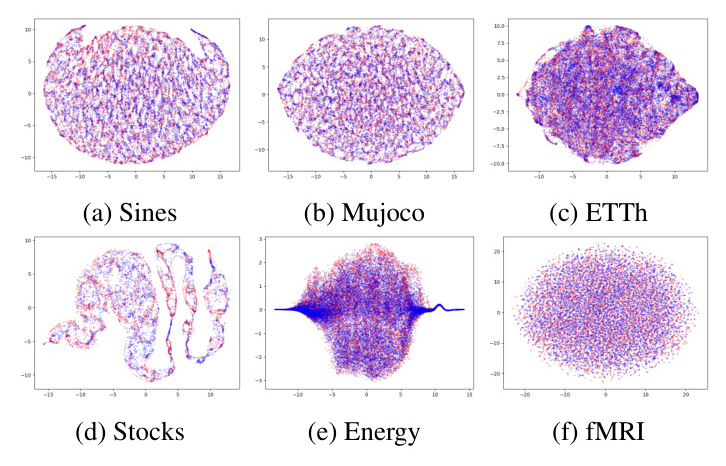
TimeBridge outperforms previous methods in unconditional generation tasks, particularly in context-FID and discriminative scores. The t-SNE plots show that the generated samples well approximate the distribution properties in complex datasets.
Synthesis with Trend Condition
The authors evaluate the performance of TimeBridge in trend-guided generation tasks using linear, polynomial, and Butterworth trends. TimeBridge achieves the best performance in Context-FID and discriminative scores, indicating its effectiveness in generating realistic data samples.
Imputation with Fixed Masks
TimeBridge also excels in imputation tasks, achieving the lowest mean squared error (MSE) and mean absolute error (MAE) compared to other models. The point-preserving sampling method ensures that the observed values are preserved during imputation.

Ablation Study
The ablation study evaluates the effectiveness of different training designs, including variance exploding (VE) scheduler, noise matching, and Fourier-based loss. The results demonstrate the importance of these components in achieving high-quality synthesis.

Conclusion
The paper highlights the effectiveness of selecting prior distributions for time series generation using diffusion bridges. TimeBridge addresses the limitations of standard Gaussian priors and provides a flexible framework for various time series synthesis tasks. Future work will explore other types of conditions, such as class labels or time-independent conditions.