Authors:
Antonio Rago、Maria Vanina Martinez
Paper:
https://arxiv.org/abs/2408.06875
Introduction
As AI models become increasingly complex and integrated into daily life, the need for interactive explainable AI (XAI) methods grows. This paper proposes using belief change theory as a formal foundation for incorporating user feedback into logical representations of data-driven classifiers. This approach aims to develop interactive explanations that promote transparency, interpretability, and accountability in human-machine interactions.
Related Work
Belief revision has been explored in various contexts. Notable contributions include:
– Falappa, Kern-Isberner, and Simari (2002): Proposed a non-prioritized revision operator using explanations by deduction.
– Coste-Marquis and Marquis (2021): Introduced a rectification operator to modify Boolean circuits to comply with background knowledge.
– Schwind, Inoue, and Marquis (2023): Developed operators for editing Boolean classifiers based on positive, negative, and combined instances.
These works provide a foundation but differ in their assumptions and approaches, particularly in handling partial and approximate knowledge and using rules rather than propositional logical sentences.
Formalising Classifiers and Explanations
Syntax
The paper formalizes classifiers’ outputs and explanations using propositional logic and formal rules. The key elements include:
– Features (F): A set of features with discrete domains.
– Classes (C): A set of possible classification labels.
– Data Points (V): Combinations of feature values.
– Classifiers (M): Mappings from data points to classes.
Semantics
The semantics for feature and classification formulas are defined using functions (I_f) and (I_c), respectively. These functions map formulas to sets of data points or classes.
Rules
Rules map feature formulas to classification formulas. They are used to represent the knowledge about a classifier and explanations.
Knowledge Base
An explanation knowledge base (K_M) consists of:
– Data (K_d): Instance rules representing known data points.
– Explanations (K_e): General rules representing behavioral patterns.
Properties
The paper defines several properties for rules and knowledge bases:
– Enforcement: A set of rules enforces another set if every assignment in the enforced set is also represented by the enforcing set.
– Consistency: A set of rules is consistent if it does not assign incompatible labels to data points.
– Coherence: A set of rules is coherent with a model if the proportion of correctly classified instances is above a threshold.
Interactive Explanations
The paper explores how interactive explanations can be modeled and deployed in real-world settings. It defines basic desiderata for incorporating user feedback:
– Constrained Inconsistency: Allowing some tolerance to inconsistency.
– Bounded Model Incoherence: Accepting a weaker notion of coherence.
– Minimal Information Loss: Minimizing modifications to the knowledge base.
Real World Scenarios
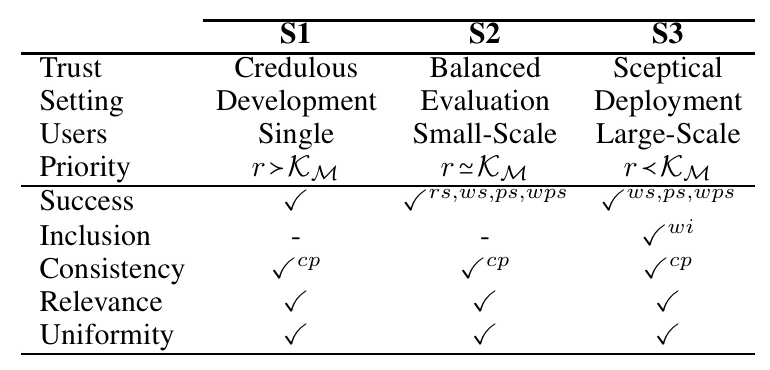
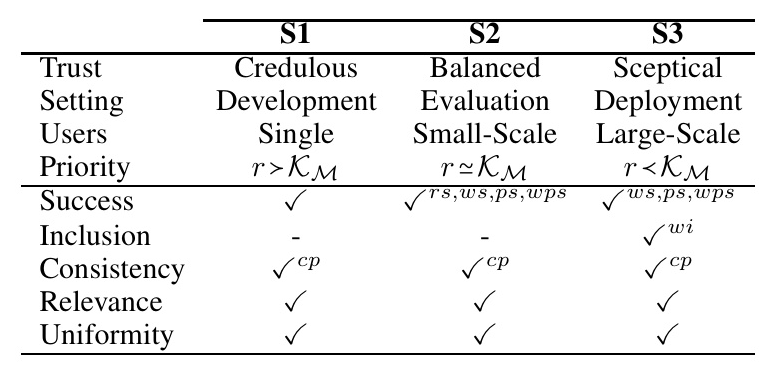
Three scenarios are considered:
1. S1 (Credulous Development): A single user provides feedback to update the model, with the feedback taking priority.
2. S2 (Balanced Evaluation): Multiple users provide feedback, balancing trust between new and existing knowledge.
3. S3 (Sceptical Deployment): Feedback from a large group of users, prioritizing existing knowledge over new feedback.
Revision of Explanation KBs
The paper analyzes a core set of belief base revision postulates and their suitability for interactive explanations:
– Success: The new knowledge is always accepted.
– Inclusion: Only the feedback is added to the existing knowledge.
– Consistency: The knowledge base becomes consistent after revision.
– Relevance: Minimal change to existing knowledge.
– Uniformity: Regularity in the effects of feedback.
Postulate Analysis
The paper evaluates the postulates for each scenario:
– S1: Prioritizes new feedback, suitable for success and relevance.
– S2: Balances new and existing knowledge, suitable for weak success and inclusion.
– S3: Prioritizes existing knowledge, suitable for weak inclusion and consistency preservation.
Discussion and Future Work
The paper suggests several avenues for future work:
– Characterizing the behavior of each setting with specific postulates.
– Implementing settings with minimal modifications to traditional belief revision operators.
– Defining alternative postulates to better satisfy the proposed desiderata.
– Exploring iterative revision and multiple revision for continuous feedback.
Conclusion
This paper proposes a novel approach to interactive XAI using belief change theory. By formalizing classifiers and explanations and analyzing belief revision postulates, it lays the groundwork for developing interactive explanations that enhance transparency, interpretability, and accountability in AI systems.